08. Natural Language Processing with TensorFlow¶

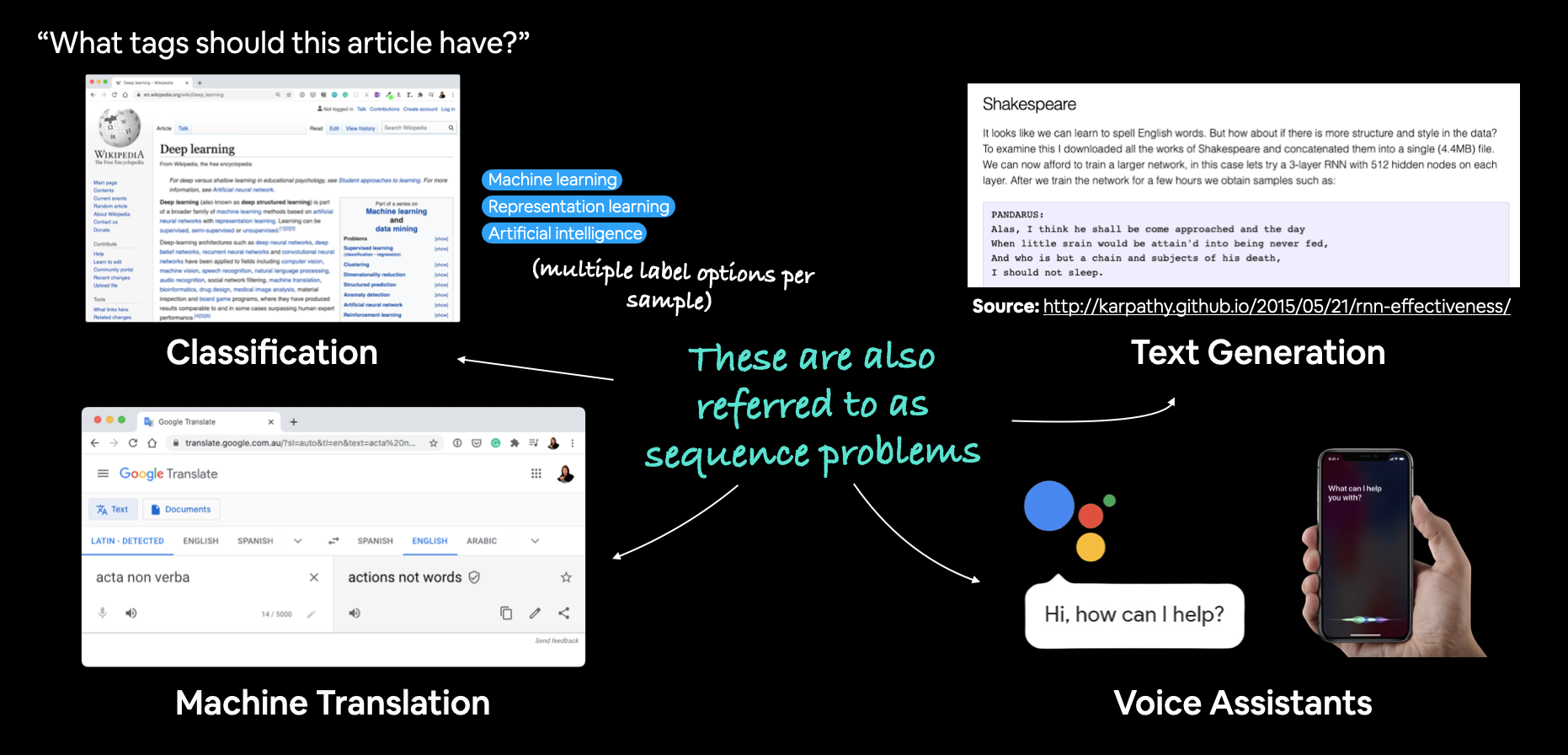A handful of example natural language processing (NLP) and natural language understanding (NLU) problems. These are also often referred to as sequence problems (going from one sequence to another).

The main goal of natural language processing (NLP) is to derive information from natural language.

Natural language is a broad term but you can consider it to cover any of the following:

• Text (such as that contained in an email, blog post, book, Tweet)
• Speech (a conversation you have with a doctor, voice commands you give to a smart speaker)

Under the umbrellas of text and speech there are many different things you might want to do.

If you're building an email application, you might want to scan incoming emails to see if they're spam or not spam (classification).

If you're trying to analyse customer feedback complaints, you might want to discover which section of your business they're for.

🔑 Note: Both of these types of data are often referred to as sequences (a sentence is a sequence of words). So a common term you'll come across in NLP problems is called seq2seq, in other words, finding information in one sequence to produce another sequence (e.g. converting a speech command to a sequence of text-based steps).

To get hands-on with NLP in TensorFlow, we're going to practice the steps we've used previously but this time with text data:

Text -> turn into numbers -> build a model -> train the model to find patterns -> use patterns (make predictions)

📖 Resource: For a great overview of NLP and the different problems within it, read the article A Simple Introduction to Natural Language Processing.

What we're going to cover¶

Let's get specific hey?

• Downloading a text dataset
• Visualizing text data
• Converting text into numbers using tokenization
• Turning our tokenized text into an embedding
• Modelling a text dataset
  • Starting with a baseline (TF-IDF)
  • Building several deep learning text models
    • Dense, LSTM, GRU, Conv1D, Transfer learning
• Comparing the performance of each our models
• Combining our models into an ensemble
• Saving and loading a trained model
• Find the most wrong predictions

How you should approach this notebook¶

You can read through the descriptions and the code (it should all run, except for the cells which error on purpose), but there's a better option.

Write all of the code yourself.

Yes. I'm serious. Create a new notebook, and rewrite each line by yourself. Investigate it, see if you can break it, why does it break?

You don't have to write the text descriptions but writing the code yourself is a great way to get hands-on experience.

Don't worry if you make mistakes, we all do. The way to get better and make less mistakes is to write more code.

📖 Resource: See the full set of course materials on GitHub: https://github.com/mrdbourke/tensorflow-deep-learning

In [1]:

import datetime
print(f"Notebook last run (end-to-end): {datetime.datetime.now()}")

import datetime print(f"Notebook last run (end-to-end): {datetime.datetime.now()}")

Notebook last run (end-to-end): 2023-05-26 00:14:41.453244

Check for GPU¶

In order for our deep learning models to run as fast as possible, we'll need access to a GPU.

In Google Colab, you can set this up by going to Runtime -> Change runtime type -> Hardware accelerator -> GPU.

After selecting GPU, you may have to restart the runtime.

In [2]:

# Check for GPU
!nvidia-smi -L

# Check for GPU !nvidia-smi -L

GPU 0: NVIDIA A100-SXM4-40GB (UUID: GPU-a07b6e3e-3ef6-217b-d41f-dc5c4d6babfd)

Get helper functions¶

In past modules, we've created a bunch of helper functions to do small tasks required for our notebooks.

Rather than rewrite all of these, we can import a script and load them in from there.

The script containing our helper functions can be found on GitHub.

In [3]:

# Download helper functions script
!wget https://raw.githubusercontent.com/mrdbourke/tensorflow-deep-learning/main/extras/helper_functions.py

# Download helper functions script !wget https://raw.githubusercontent.com/mrdbourke/tensorflow-deep-learning/main/extras/helper_functions.py

--2023-05-26 00:14:41--  https://raw.githubusercontent.com/mrdbourke/tensorflow-deep-learning/main/extras/helper_functions.py
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 185.199.108.133, 185.199.109.133, 185.199.110.133, ...
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|185.199.108.133|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 10246 (10K) [text/plain]
Saving to: ‘helper_functions.py’

helper_functions.py 100%[===================>]  10.01K  --.-KB/s    in 0s      

2023-05-26 00:14:41 (94.5 MB/s) - ‘helper_functions.py’ saved [10246/10246]

In [4]:

# Import series of helper functions for the notebook
from helper_functions import unzip_data, create_tensorboard_callback, plot_loss_curves, compare_historys

# Import series of helper functions for the notebook from helper_functions import unzip_data, create_tensorboard_callback, plot_loss_curves, compare_historys

Download a text dataset¶

Let's start by download a text dataset. We'll be using the Real or Not? dataset from Kaggle which contains text-based Tweets about natural disasters.

The Real Tweets are actually about disasters, for example:

Jetstar and Virgin forced to cancel Bali flights again because of ash from Mount Raung volcano

The Not Real Tweets are Tweets not about disasters (they can be on anything), for example:

'Education is the most powerful weapon which you can use to change the world.' Nelson #Mandela #quote

For convenience, the dataset has been downloaded from Kaggle (doing this requires a Kaggle account) and uploaded as a downloadable zip file.

🔑 Note: The original downloaded data has not been altered to how you would download it from Kaggle.

In [5]:

# Download data (same as from Kaggle)
!wget "https://storage.googleapis.com/ztm_tf_course/nlp_getting_started.zip"

# Unzip data
unzip_data("nlp_getting_started.zip")

# Download data (same as from Kaggle) !wget "https://storage.googleapis.com/ztm_tf_course/nlp_getting_started.zip" # Unzip data unzip_data("nlp_getting_started.zip")

--2023-05-26 00:14:45--  https://storage.googleapis.com/ztm_tf_course/nlp_getting_started.zip
Resolving storage.googleapis.com (storage.googleapis.com)... 172.217.194.128, 74.125.200.128, 74.125.68.128, ...
Connecting to storage.googleapis.com (storage.googleapis.com)|172.217.194.128|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 607343 (593K) [application/zip]
Saving to: ‘nlp_getting_started.zip’

nlp_getting_started 100%[===================>] 593.11K   731KB/s    in 0.8s    

2023-05-26 00:14:46 (731 KB/s) - ‘nlp_getting_started.zip’ saved [607343/607343]

Unzipping nlp_getting_started.zip gives the following 3 .csv files:

• sample_submission.csv - an example of the file you'd submit to the Kaggle competition of your model's predictions.
• train.csv - training samples of real and not real diaster Tweets.
• test.csv - testing samples of real and not real diaster Tweets.

Visualizing a text dataset¶

Once you've acquired a new dataset to work with, what should you do first?

Explore it? Inspect it? Verify it? Become one with it?

All correct.

Remember the motto: visualize, visualize, visualize.

Right now, our text data samples are in the form of .csv files. For an easy way to make them visual, let's turn them into pandas DataFrame's.

📖 Reading: You might come across text datasets in many different formats. Aside from CSV files (what we're working with), you'll probably encounter .txt files and .json files too. For working with these type of files, I'd recommend reading the two following articles by RealPython:

• How to Read and Write Files in Python
• Working with JSON Data in Python

In [6]:

# Turn .csv files into pandas DataFrame's
import pandas as pd
train_df = pd.read_csv("train.csv")
test_df = pd.read_csv("test.csv")
train_df.head()

# Turn .csv files into pandas DataFrame's import pandas as pd train_df = pd.read_csv("train.csv") test_df = pd.read_csv("test.csv") train_df.head()

Out[6]:

	id	keyword	location	text	target
0	1	NaN	NaN	Our Deeds are the Reason of this #earthquake M...	1
1	4	NaN	NaN	Forest fire near La Ronge Sask. Canada	1
2	5	NaN	NaN	All residents asked to 'shelter in place' are ...	1
3	6	NaN	NaN	13,000 people receive #wildfires evacuation or...	1
4	7	NaN	NaN	Just got sent this photo from Ruby #Alaska as ...	1

The training data we downloaded is probably shuffled already. But just to be sure, let's shuffle it again.

In [7]:

# Shuffle training dataframe
train_df_shuffled = train_df.sample(frac=1, random_state=42) # shuffle with random_state=42 for reproducibility
train_df_shuffled.head()

# Shuffle training dataframe train_df_shuffled = train_df.sample(frac=1, random_state=42) # shuffle with random_state=42 for reproducibility train_df_shuffled.head()

Out[7]:

	id	keyword	location	text	target
2644	3796	destruction	NaN	So you have a new weapon that can cause un-ima...	1
2227	3185	deluge	NaN	The f$&@ing things I do for #GISHWHES Just...	0
5448	7769	police	UK	DT @georgegalloway: RT @Galloway4Mayor: ‰ÛÏThe...	1
132	191	aftershock	NaN	Aftershock back to school kick off was great. ...	0
6845	9810	trauma	Montgomery County, MD	in response to trauma Children of Addicts deve...	0

Notice how the training data has a "target" column.

We're going to be writing code to find patterns (e.g. different combinations of words) in the "text" column of the training dataset to predict the value of the "target" column.

The test dataset doesn't have a "target" column.

Inputs (text column) -> Machine Learning Algorithm -> Outputs (target column)

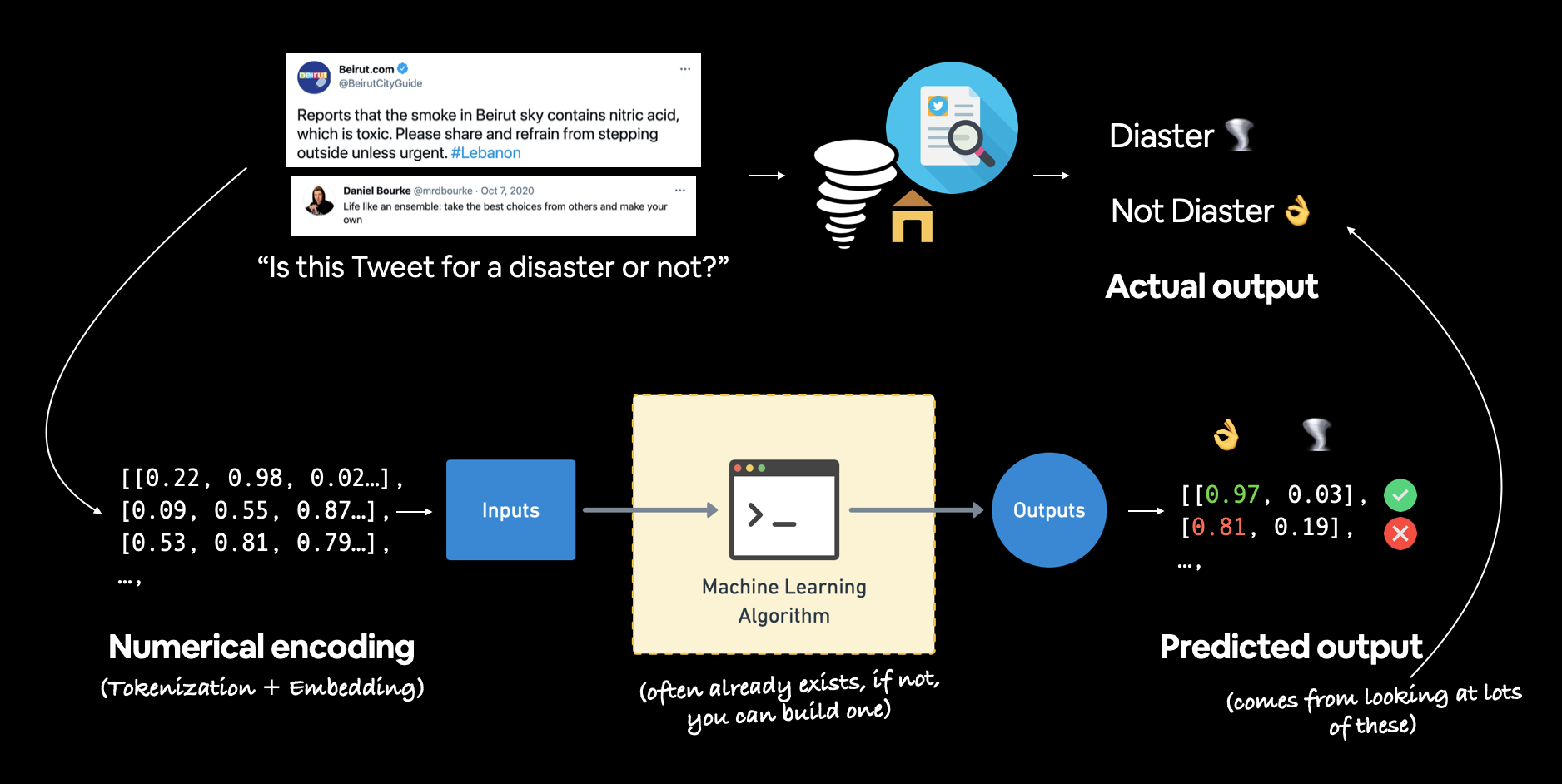Example text classification inputs and outputs for the problem of classifying whether a Tweet is about a disaster or not.

In [8]:

# The test data doesn't have a target (that's what we'd try to predict)
test_df.head()

# The test data doesn't have a target (that's what we'd try to predict) test_df.head()

Out[8]:

	id	keyword	location	text
0	0	NaN	NaN	Just happened a terrible car crash
1	2	NaN	NaN	Heard about #earthquake is different cities, s...
2	3	NaN	NaN	there is a forest fire at spot pond, geese are...
3	9	NaN	NaN	Apocalypse lighting. #Spokane #wildfires
4	11	NaN	NaN	Typhoon Soudelor kills 28 in China and Taiwan

Let's check how many examples of each target we have.

In [9]:

# How many examples of each class?
train_df.target.value_counts()

# How many examples of each class? train_df.target.value_counts()

Out[9]:

0    4342
1    3271
Name: target, dtype: int64

Since we have two target values, we're dealing with a binary classification problem.

It's fairly balanced too, about 60% negative class (target = 0) and 40% positive class (target = 1).

Where,

• 1 = a real disaster Tweet
• 0 = not a real disaster Tweet

And what about the total number of samples we have?

In [10]:

# How many samples total?
print(f"Total training samples: {len(train_df)}")
print(f"Total test samples: {len(test_df)}")
print(f"Total samples: {len(train_df) + len(test_df)}")

# How many samples total? print(f"Total training samples: {len(train_df)}") print(f"Total test samples: {len(test_df)}") print(f"Total samples: {len(train_df) + len(test_df)}")

Total training samples: 7613
Total test samples: 3263
Total samples: 10876

Alright, seems like we've got a decent amount of training and test data. If anything, we've got an abundance of testing examples, usually a split of 90/10 (90% training, 10% testing) or 80/20 is suffice.

Okay, time to visualize, let's write some code to visualize random text samples.

🤔 Question: Why visualize random samples? You could visualize samples in order but this could lead to only seeing a certain subset of data. Better to visualize a substantial quantity (100+) of random samples to get an idea of the different kinds of data you're working with. In machine learning, never underestimate the power of randomness.

In [11]:

# Let's visualize some random training examples
import random
random_index = random.randint(0, len(train_df)-5) # create random indexes not higher than the total number of samples
for row in train_df_shuffled[["text", "target"]][random_index:random_index+5].itertuples():
  _, text, target = row
  print(f"Target: {target}", "(real disaster)" if target > 0 else "(not real disaster)")
  print(f"Text:\n{text}\n")
  print("---\n")

# Let's visualize some random training examples import random random_index = random.randint(0, len(train_df)-5) # create random indexes not higher than the total number of samples for row in train_df_shuffled[["text", "target"]][random_index:random_index+5].itertuples(): _, text, target = row print(f"Target: {target}", "(real disaster)" if target > 0 else "(not real disaster)") print(f"Text:\n{text}\n") print("---\n")

Target: 0 (not real disaster)
Text:
@JamesMelville Some old testimony of weapons used to promote conflicts
Tactics - corruption & infiltration of groups
https://t.co/cyU8zxw1oH

---

Target: 1 (real disaster)
Text:
Now Trending in Nigeria: Police charge traditional ruler others with informant‰Ûªs  murder http://t.co/93inFxzhX0

---

Target: 1 (real disaster)
Text:
REPORTED: HIT & RUN-IN ROADWAY-PROPERTY DAMAGE at 15901 STATESVILLE RD

---

Target: 1 (real disaster)
Text:
ohH NO FUKURODANI DIDN'T SURVIVE THE APOCALYPSE BOKUTO FEELS HORRIBLE  my poor boy my ppor child

---

Target: 1 (real disaster)
Text:
Maryland mansion fire that killed 6 caused by damaged plug under Christmas tree report says - Into the flames: Firefighter's bravery...

---

Split data into training and validation sets¶

Since the test set has no labels and we need a way to evalaute our trained models, we'll split off some of the training data and create a validation set.

When our model trains (tries patterns in the Tweet samples), it'll only see data from the training set and we can see how it performs on unseen data using the validation set.

We'll convert our splits from pandas Series datatypes to lists of strings (for the text) and lists of ints (for the labels) for ease of use later.

To split our training dataset and create a validation dataset, we'll use Scikit-Learn's train_test_split() method and dedicate 10% of the training samples to the validation set.

In [12]:

from sklearn.model_selection import train_test_split

# Use train_test_split to split training data into training and validation sets
train_sentences, val_sentences, train_labels, val_labels = train_test_split(train_df_shuffled["text"].to_numpy(),
                                                                            train_df_shuffled["target"].to_numpy(),
                                                                            test_size=0.1, # dedicate 10% of samples to validation set
                                                                            random_state=42) # random state for reproducibility

from sklearn.model_selection import train_test_split # Use train_test_split to split training data into training and validation sets train_sentences, val_sentences, train_labels, val_labels = train_test_split(train_df_shuffled["text"].to_numpy(), train_df_shuffled["target"].to_numpy(), test_size=0.1, # dedicate 10% of samples to validation set random_state=42) # random state for reproducibility

In [13]:

# Check the lengths
len(train_sentences), len(train_labels), len(val_sentences), len(val_labels)

# Check the lengths len(train_sentences), len(train_labels), len(val_sentences), len(val_labels)

Out[13]:

(6851, 6851, 762, 762)

In [14]:

# View the first 10 training sentences and their labels
train_sentences[:10], train_labels[:10]

# View the first 10 training sentences and their labels train_sentences[:10], train_labels[:10]

Out[14]:

(array(['@mogacola @zamtriossu i screamed after hitting tweet',
        'Imagine getting flattened by Kurt Zouma',
        '@Gurmeetramrahim #MSGDoing111WelfareWorks Green S welfare force ke appx 65000 members har time disaster victim ki help ke liye tyar hai....',
        "@shakjn @C7 @Magnums im shaking in fear he's gonna hack the planet",
        'Somehow find you and I collide http://t.co/Ee8RpOahPk',
        '@EvaHanderek @MarleyKnysh great times until the bus driver held us hostage in the mall parking lot lmfao',
        'destroy the free fandom honestly',
        'Weapons stolen from National Guard Armory in New Albany still missing #Gunsense http://t.co/lKNU8902JE',
        '@wfaaweather Pete when will the heat wave pass? Is it really going to be mid month? Frisco Boy Scouts have a canoe trip in Okla.',
        'Patient-reported outcomes in long-term survivors of metastatic colorectal cancer - British Journal of Surgery http://t.co/5Yl4DC1Tqt'],
       dtype=object),
 array([0, 0, 1, 0, 0, 1, 1, 0, 1, 1]))

Converting text into numbers¶

Wonderful! We've got a training set and a validation set containing Tweets and labels.

Our labels are in numerical form (0 and 1) but our Tweets are in string form.

🤔 Question: What do you think we have to do before we can use a machine learning algorithm with our text data?

If you answered something along the lines of "turn it into numbers", you're correct. A machine learning algorithm requires its inputs to be in numerical form.

In NLP, there are two main concepts for turning text into numbers:

• Tokenization - A straight mapping from word or character or sub-word to a numerical value. There are three main levels of tokenization:
  1. Using word-level tokenization with the sentence "I love TensorFlow" might result in "I" being 0, "love" being 1 and "TensorFlow" being 2. In this case, every word in a sequence considered a single token.
  2. Character-level tokenization, such as converting the letters A-Z to values 1-26. In this case, every character in a sequence considered a single token.
  3. Sub-word tokenization is in between word-level and character-level tokenization. It involves breaking invidual words into smaller parts and then converting those smaller parts into numbers. For example, "my favourite food is pineapple pizza" might become "my, fav, avour, rite, fo, oo, od, is, pin, ine, app, le, piz, za". After doing this, these sub-words would then be mapped to a numerical value. In this case, every word could be considered multiple tokens.
• Embeddings - An embedding is a representation of natural language which can be learned. Representation comes in the form of a feature vector. For example, the word "dance" could be represented by the 5-dimensional vector [-0.8547, 0.4559, -0.3332, 0.9877, 0.1112]. It's important to note here, the size of the feature vector is tuneable. There are two ways to use embeddings:
  1. Create your own embedding - Once your text has been turned into numbers (required for an embedding), you can put them through an embedding layer (such as tf.keras.layers.Embedding) and an embedding representation will be learned during model training.
  2. Reuse a pre-learned embedding - Many pre-trained embeddings exist online. These pre-trained embeddings have often been learned on large corpuses of text (such as all of Wikipedia) and thus have a good underlying representation of natural language. You can use a pre-trained embedding to initialize your model and fine-tune it to your own specific task.

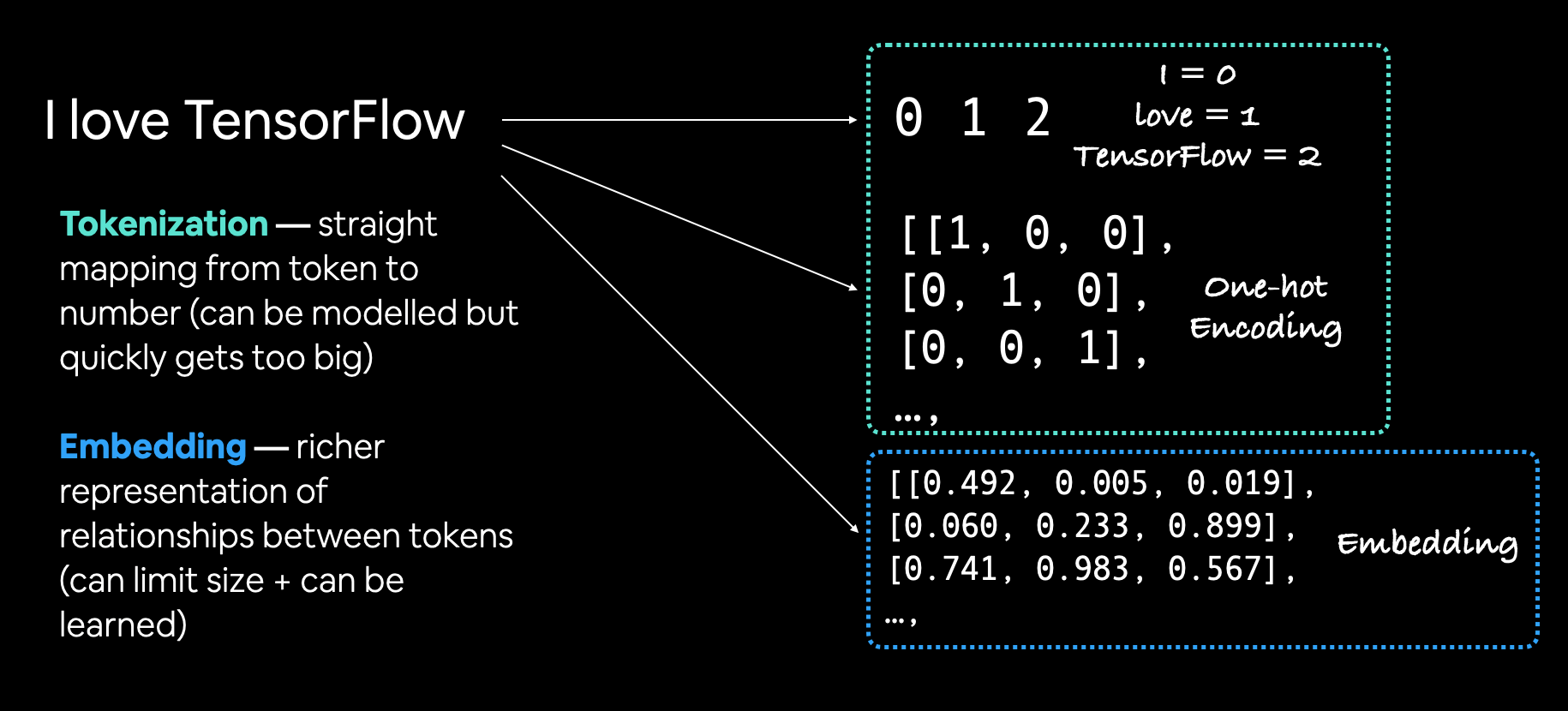Example of tokenization (straight mapping from word to number) and embedding (richer representation of relationships between tokens).

🤔 Question: What level of tokenzation should I use? What embedding should should I choose?

It depends on your problem. You could try character-level tokenization/embeddings and word-level tokenization/embeddings and see which perform best. You might even want to try stacking them (e.g. combining the outputs of your embedding layers using tf.keras.layers.concatenate).

If you're looking for pre-trained word embeddings, Word2vec embeddings, GloVe embeddings and many of the options available on TensorFlow Hub are great places to start.

🔑 Note: Much like searching for a pre-trained computer vision model, you can search for pre-trained word embeddings to use for your problem. Try searching for something like "use pre-trained word embeddings in TensorFlow".

Text vectorization (tokenization)¶

Enough talking about tokenization and embeddings, let's create some.

We'll practice tokenzation (mapping our words to numbers) first.

To tokenize our words, we'll use the helpful preprocessing layer tf.keras.layers.experimental.preprocessing.TextVectorization.

The TextVectorization layer takes the following parameters:

• max_tokens - The maximum number of words in your vocabulary (e.g. 20000 or the number of unique words in your text), includes a value for OOV (out of vocabulary) tokens.
• standardize - Method for standardizing text. Default is "lower_and_strip_punctuation" which lowers text and removes all punctuation marks.
• split - How to split text, default is "whitespace" which splits on spaces.
• ngrams - How many words to contain per token split, for example, ngrams=2 splits tokens into continuous sequences of 2.
• output_mode - How to output tokens, can be "int" (integer mapping), "binary" (one-hot encoding), "count" or "tf-idf". See documentation for more.
• output_sequence_length - Length of tokenized sequence to output. For example, if output_sequence_length=150, all tokenized sequences will be 150 tokens long.
• pad_to_max_tokens - Defaults to False, if True, the output feature axis will be padded to max_tokens even if the number of unique tokens in the vocabulary is less than max_tokens. Only valid in certain modes, see docs for more.

Let's see it in action.

In [15]:

import tensorflow as tf
from tensorflow.keras.layers import TextVectorization # after TensorFlow 2.6

# Before TensorFlow 2.6
# from tensorflow.keras.layers.experimental.preprocessing import TextVectorization 
# Note: in TensorFlow 2.6+, you no longer need "layers.experimental.preprocessing"
# you can use: "tf.keras.layers.TextVectorization", see https://github.com/tensorflow/tensorflow/releases/tag/v2.6.0 for more

# Use the default TextVectorization variables
text_vectorizer = TextVectorization(max_tokens=None, # how many words in the vocabulary (all of the different words in your text)
                                    standardize="lower_and_strip_punctuation", # how to process text
                                    split="whitespace", # how to split tokens
                                    ngrams=None, # create groups of n-words?
                                    output_mode="int", # how to map tokens to numbers
                                    output_sequence_length=None) # how long should the output sequence of tokens be?
                                    # pad_to_max_tokens=True) # Not valid if using max_tokens=None

import tensorflow as tf from tensorflow.keras.layers import TextVectorization # after TensorFlow 2.6 # Before TensorFlow 2.6 # from tensorflow.keras.layers.experimental.preprocessing import TextVectorization # Note: in TensorFlow 2.6+, you no longer need "layers.experimental.preprocessing" # you can use: "tf.keras.layers.TextVectorization", see https://github.com/tensorflow/tensorflow/releases/tag/v2.6.0 for more # Use the default TextVectorization variables text_vectorizer = TextVectorization(max_tokens=None, # how many words in the vocabulary (all of the different words in your text) standardize="lower_and_strip_punctuation", # how to process text split="whitespace", # how to split tokens ngrams=None, # create groups of n-words? output_mode="int", # how to map tokens to numbers output_sequence_length=None) # how long should the output sequence of tokens be? # pad_to_max_tokens=True) # Not valid if using max_tokens=None

We've initialized a TextVectorization object with the default settings but let's customize it a little bit for our own use case.

In particular, let's set values for max_tokens and output_sequence_length.

For max_tokens (the number of words in the vocabulary), multiples of 10,000 (10,000, 20,000, 30,000) or the exact number of unique words in your text (e.g. 32,179) are common values.

For our use case, we'll use 10,000.

And for the output_sequence_length we'll use the average number of tokens per Tweet in the training set. But first, we'll need to find it.

In [16]:

# Find average number of tokens (words) in training Tweets
round(sum([len(i.split()) for i in train_sentences])/len(train_sentences))

# Find average number of tokens (words) in training Tweets round(sum([len(i.split()) for i in train_sentences])/len(train_sentences))

Out[16]:

15

Now let's create another TextVectorization object using our custom parameters.

In [17]:

# Setup text vectorization with custom variables
max_vocab_length = 10000 # max number of words to have in our vocabulary
max_length = 15 # max length our sequences will be (e.g. how many words from a Tweet does our model see?)

text_vectorizer = TextVectorization(max_tokens=max_vocab_length,
                                    output_mode="int",
                                    output_sequence_length=max_length)

# Setup text vectorization with custom variables max_vocab_length = 10000 # max number of words to have in our vocabulary max_length = 15 # max length our sequences will be (e.g. how many words from a Tweet does our model see?) text_vectorizer = TextVectorization(max_tokens=max_vocab_length, output_mode="int", output_sequence_length=max_length)

Beautiful!

To map our TextVectorization instance text_vectorizer to our data, we can call the adapt() method on it whilst passing it our training text.

In [18]:

# Fit the text vectorizer to the training text
text_vectorizer.adapt(train_sentences)

# Fit the text vectorizer to the training text text_vectorizer.adapt(train_sentences)

Training data mapped! Let's try our text_vectorizer on a custom sentence (one similar to what you might see in the training data).

In [19]:

# Create sample sentence and tokenize it
sample_sentence = "There's a flood in my street!"
text_vectorizer([sample_sentence])

# Create sample sentence and tokenize it sample_sentence = "There's a flood in my street!" text_vectorizer([sample_sentence])

Out[19]:

<tf.Tensor: shape=(1, 15), dtype=int64, numpy=
array([[264,   3, 232,   4,  13, 698,   0,   0,   0,   0,   0,   0,   0,
          0,   0]])>

Wonderful, it seems we've got a way to turn our text into numbers (in this case, word-level tokenization). Notice the 0's at the end of the returned tensor, this is because we set output_sequence_length=15, meaning no matter the size of the sequence we pass to text_vectorizer, it always returns a sequence with a length of 15.

How about we try our text_vectorizer on a few random sentences?

In [20]:

# Choose a random sentence from the training dataset and tokenize it
random_sentence = random.choice(train_sentences)
print(f"Original text:\n{random_sentence}\
      \n\nVectorized version:")
text_vectorizer([random_sentence])

# Choose a random sentence from the training dataset and tokenize it random_sentence = random.choice(train_sentences) print(f"Original text:\n{random_sentence}\ \n\nVectorized version:") text_vectorizer([random_sentence])

Original text:
new summer long thin body bag hip A word skirt Blue http://t.co/lvKoEMsq8m http://t.co/CjiRhHh4vj      

Vectorized version:

Out[20]:

<tf.Tensor: shape=(1, 15), dtype=int64, numpy=
array([[  50,  270,  480, 3335,   83,  322, 2436,    3, 1448, 3407,  824,
           1,    1,    0,    0]])>

Looking good!

Finally, we can check the unique tokens in our vocabulary using the get_vocabulary() method.

In [21]:

# Get the unique words in the vocabulary
words_in_vocab = text_vectorizer.get_vocabulary()
top_5_words = words_in_vocab[:5] # most common tokens (notice the [UNK] token for "unknown" words)
bottom_5_words = words_in_vocab[-5:] # least common tokens
print(f"Number of words in vocab: {len(words_in_vocab)}")
print(f"Top 5 most common words: {top_5_words}") 
print(f"Bottom 5 least common words: {bottom_5_words}")

# Get the unique words in the vocabulary words_in_vocab = text_vectorizer.get_vocabulary() top_5_words = words_in_vocab[:5] # most common tokens (notice the [UNK] token for "unknown" words) bottom_5_words = words_in_vocab[-5:] # least common tokens print(f"Number of words in vocab: {len(words_in_vocab)}") print(f"Top 5 most common words: {top_5_words}") print(f"Bottom 5 least common words: {bottom_5_words}")

Number of words in vocab: 10000
Top 5 most common words: ['', '[UNK]', 'the', 'a', 'in']
Bottom 5 least common words: ['pages', 'paeds', 'pads', 'padres', 'paddytomlinson1']

Creating an Embedding using an Embedding Layer¶

We've got a way to map our text to numbers. How about we go a step further and turn those numbers into an embedding?

The powerful thing about an embedding is it can be learned during training. This means rather than just being static (e.g. 1 = I, 2 = love, 3 = TensorFlow), a word's numeric representation can be improved as a model goes through data samples.

We can see what an embedding of a word looks like by using the tf.keras.layers.Embedding layer.

The main parameters we're concerned about here are:

• input_dim - The size of the vocabulary (e.g. len(text_vectorizer.get_vocabulary()).
• output_dim - The size of the output embedding vector, for example, a value of 100 outputs a feature vector of size 100 for each word.
• embeddings_initializer - How to initialize the embeddings matrix, default is "uniform" which randomly initalizes embedding matrix with uniform distribution. This can be changed for using pre-learned embeddings.
• input_length - Length of sequences being passed to embedding layer.

Knowing these, let's make an embedding layer.

In [22]:

tf.random.set_seed(42)
from tensorflow.keras import layers

embedding = layers.Embedding(input_dim=max_vocab_length, # set input shape
                             output_dim=128, # set size of embedding vector
                             embeddings_initializer="uniform", # default, intialize randomly
                             input_length=max_length, # how long is each input
                             name="embedding_1") 

embedding

tf.random.set_seed(42) from tensorflow.keras import layers embedding = layers.Embedding(input_dim=max_vocab_length, # set input shape output_dim=128, # set size of embedding vector embeddings_initializer="uniform", # default, intialize randomly input_length=max_length, # how long is each input name="embedding_1") embedding

Out[22]:

<keras.layers.core.embedding.Embedding at 0x7f0c118dcc40>

Excellent, notice how embedding is a TensoFlow layer? This is important because we can use it as part of a model, meaning its parameters (word representations) can be updated and improved as the model learns.

How about we try it out on a sample sentence?

In [23]:

# Get a random sentence from training set
random_sentence = random.choice(train_sentences)
print(f"Original text:\n{random_sentence}\
      \n\nEmbedded version:")

# Embed the random sentence (turn it into numerical representation)
sample_embed = embedding(text_vectorizer([random_sentence]))
sample_embed

# Get a random sentence from training set random_sentence = random.choice(train_sentences) print(f"Original text:\n{random_sentence}\ \n\nEmbedded version:") # Embed the random sentence (turn it into numerical representation) sample_embed = embedding(text_vectorizer([random_sentence])) sample_embed

Original text:
Now on #ComDev #Asia: Radio stations in #Bangladesh broadcasting #programs ?to address the upcoming cyclone #komen http://t.co/iOVr4yMLKp      

Embedded version:

Out[23]:

<tf.Tensor: shape=(1, 15, 128), dtype=float32, numpy=
array([[[-0.04868475, -0.03902867, -0.01375594, ...,  0.01682534,
         -0.0439401 , -0.04604518],
        [-0.04827927, -0.00328457,  0.02171678, ..., -0.03261749,
         -0.01061803, -0.0481179 ],
        [-0.02431345,  0.01104342,  0.00933889, ..., -0.04607272,
         -0.00651377,  0.03853123],
        ...,
        [-0.03270339,  0.03608486,  0.03573406, ...,  0.03622421,
          0.03427652, -0.03483479],
        [-0.0489977 ,  0.01962234,  0.02186165, ...,  0.03139002,
         -0.00744159,  0.0428594 ],
        [ 0.01265842,  0.02462569, -0.04731182, ...,  0.00403734,
          0.0431679 ,  0.03959754]]], dtype=float32)>

Each token in the sentence gets turned into a length 128 feature vector.

In [24]:

# Check out a single token's embedding
sample_embed[0][0]

# Check out a single token's embedding sample_embed[0][0]

Out[24]:

<tf.Tensor: shape=(128,), dtype=float32, numpy=
array([-0.04868475, -0.03902867, -0.01375594,  0.01587117, -0.02964617,
        0.00738639, -0.03109504,  0.03008839, -0.01458266, -0.03069887,
       -0.04926676, -0.03454053, -0.04019499, -0.04406711,  0.01975099,
        0.02852687, -0.04052209, -0.03800124,  0.03438697, -0.0118026 ,
       -0.03470664, -0.01146972,  0.0449667 , -0.00269016,  0.02131964,
       -0.04141569, -0.03724197,  0.01624352,  0.03269556,  0.03813741,
        0.03606123,  0.00698509, -0.03569689,  0.02056131, -0.03467314,
        0.01110398,  0.02095172,  0.02219674, -0.04576088, -0.04229112,
       -0.02345047,  0.02578488,  0.02985479, -0.00203061,  0.03920727,
        0.04065951,  0.03973453,  0.03947322,  0.01699554,  0.0021927 ,
        0.03676197, -0.04327145,  0.02495482,  0.02447238, -0.04413594,
       -0.01388069, -0.00375951, -0.0328602 , -0.00067427,  0.01808068,
        0.04227355,  0.02817165,  0.01965401, -0.01514393,  0.01905935,
       -0.03820103, -0.04916845,  0.02303007,  0.00830983,  0.01011454,
       -0.04043181,  0.02080727, -0.03319015,  0.04188809, -0.01183917,
       -0.01822531, -0.02172413,  0.03059311,  0.02727925, -0.00328885,
       -0.00808424, -0.02095444, -0.00894216,  0.00770078, -0.00439024,
        0.03637768,  0.02007255, -0.02650907, -0.01374531,  0.01806785,
       -0.03309877, -0.01076321, -0.04107616,  0.01709371,  0.04567242,
       -0.01824218,  0.02805582,  0.02974418, -0.04001283, -0.04077357,
        0.00323737,  0.04038842, -0.00992844, -0.03974843,  0.04533138,
        0.04738795,  0.02837384,  0.03874009, -0.01673441, -0.00258055,
       -0.01975214, -0.04166807, -0.02483889, -0.02804886,  0.04608755,
        0.03544754,  0.02697959,  0.00242041,  0.00101637, -0.01162767,
       -0.00497937,  0.00540714, -0.01258825,  0.00779672,  0.02742722,
        0.01682534, -0.0439401 , -0.04604518], dtype=float32)>

These values might not mean much to us but they're what our computer sees each word as. When our model looks for patterns in different samples, these values will be updated as necessary.

🔑 Note: The previous two concepts (tokenization and embeddings) are the foundation for many NLP tasks. So if you're not sure about anything, be sure to research and conduct your own experiments to further help your understanding.

Modelling a text dataset¶

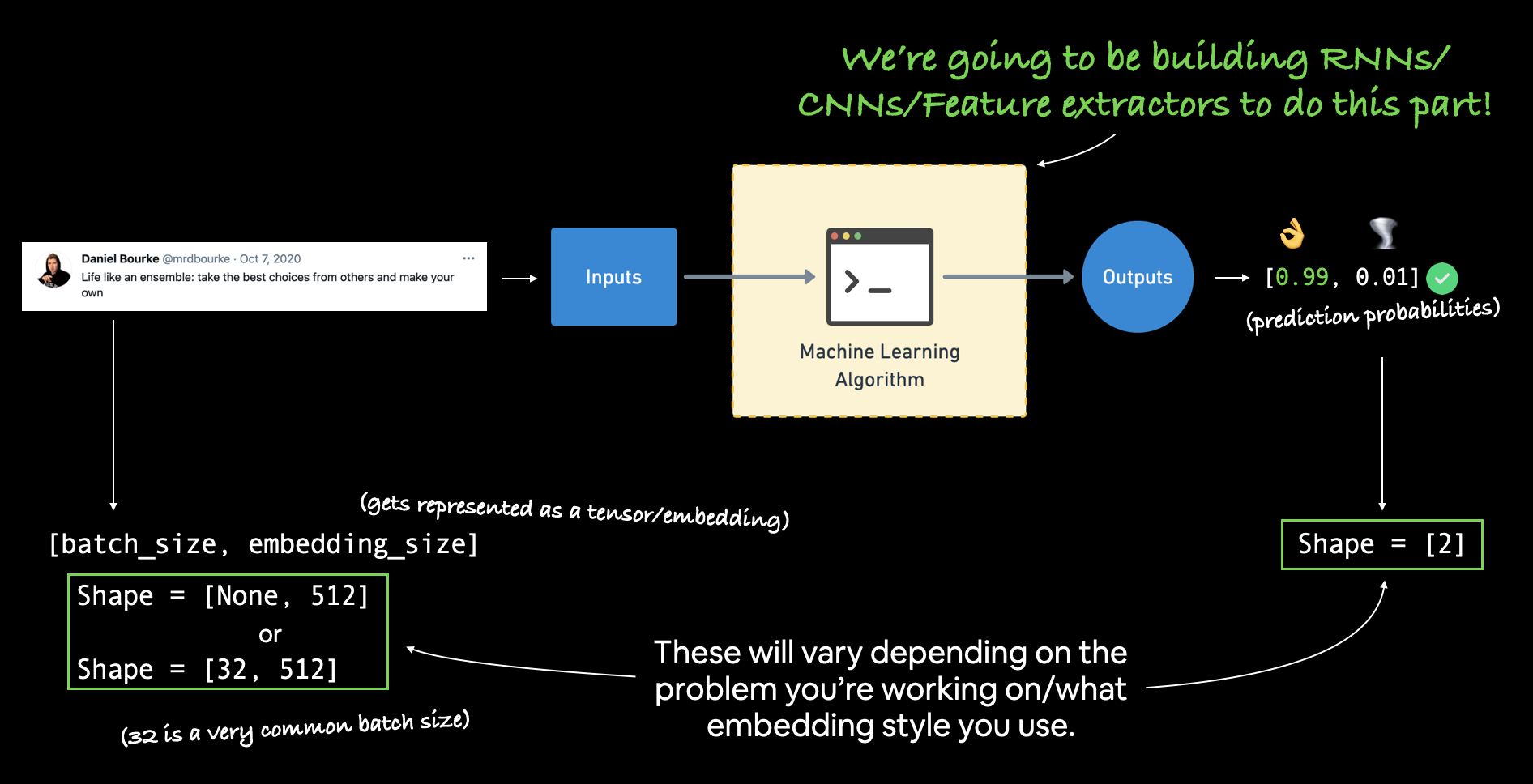Once you've got your inputs and outputs prepared, it's a matter of figuring out which machine learning model to build in between them to bridge the gap.

Now that we've got a way to turn our text data into numbers, we can start to build machine learning models to model it.

To get plenty of practice, we're going to build a series of different models, each as its own experiment. We'll then compare the results of each model and see which one performed best.

More specifically, we'll be building the following:

• Model 0: Naive Bayes (baseline)
• Model 1: Feed-forward neural network (dense model)
• Model 2: LSTM model
• Model 3: GRU model
• Model 4: Bidirectional-LSTM model
• Model 5: 1D Convolutional Neural Network
• Model 6: TensorFlow Hub Pretrained Feature Extractor
• Model 7: Same as model 6 with 10% of training data

Model 0 is the simplest to acquire a baseline which we'll expect each other of the other deeper models to beat.

Each experiment will go through the following steps:

• Construct the model
• Train the model
• Make predictions with the model
• Track prediction evaluation metrics for later comparison

Let's get started.

Model 0: Getting a baseline¶

As with all machine learning modelling experiments, it's important to create a baseline model so you've got a benchmark for future experiments to build upon.

To create our baseline, we'll create a Scikit-Learn Pipeline using the TF-IDF (term frequency-inverse document frequency) formula to convert our words to numbers and then model them with the Multinomial Naive Bayes algorithm. This was chosen via referring to the Scikit-Learn machine learning map.

📖 Reading: The ins and outs of TF-IDF algorithm is beyond the scope of this notebook, however, the curious reader is encouraged to check out the Scikit-Learn documentation for more.

In [25]:

from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import Pipeline

# Create tokenization and modelling pipeline
model_0 = Pipeline([
                    ("tfidf", TfidfVectorizer()), # convert words to numbers using tfidf
                    ("clf", MultinomialNB()) # model the text
])

# Fit the pipeline to the training data
model_0.fit(train_sentences, train_labels)

from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.naive_bayes import MultinomialNB from sklearn.pipeline import Pipeline # Create tokenization and modelling pipeline model_0 = Pipeline([ ("tfidf", TfidfVectorizer()), # convert words to numbers using tfidf ("clf", MultinomialNB()) # model the text ]) # Fit the pipeline to the training data model_0.fit(train_sentences, train_labels)

Out[25]:

Pipeline(steps=[('tfidf', TfidfVectorizer()), ('clf', MultinomialNB())])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

The benefit of using a shallow model like Multinomial Naive Bayes is that training is very fast.

Let's evaluate our model and find our baseline metric.

In [26]:

baseline_score = model_0.score(val_sentences, val_labels)
print(f"Our baseline model achieves an accuracy of: {baseline_score*100:.2f}%")

baseline_score = model_0.score(val_sentences, val_labels) print(f"Our baseline model achieves an accuracy of: {baseline_score*100:.2f}%")

Our baseline model achieves an accuracy of: 79.27%

How about we make some predictions with our baseline model?

In [27]:

# Make predictions
baseline_preds = model_0.predict(val_sentences)
baseline_preds[:20]

# Make predictions baseline_preds = model_0.predict(val_sentences) baseline_preds[:20]

Out[27]:

array([1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1])

Creating an evaluation function for our model experiments¶

We could evaluate these as they are but since we're going to be evaluating several models in the same way going forward, let's create a helper function which takes an array of predictions and ground truth labels and computes the following:

• Accuracy
• Precision
• Recall
• F1-score

🔑 Note: Since we're dealing with a classification problem, the above metrics are the most appropriate. If we were working with a regression problem, other metrics such as MAE (mean absolute error) would be a better choice.

In [28]:

# Function to evaluate: accuracy, precision, recall, f1-score
from sklearn.metrics import accuracy_score, precision_recall_fscore_support

def calculate_results(y_true, y_pred):
  """
  Calculates model accuracy, precision, recall and f1 score of a binary classification model.

  Args:
  -----
  y_true = true labels in the form of a 1D array
  y_pred = predicted labels in the form of a 1D array

  Returns a dictionary of accuracy, precision, recall, f1-score.
  """
  # Calculate model accuracy
  model_accuracy = accuracy_score(y_true, y_pred) * 100
  # Calculate model precision, recall and f1 score using "weighted" average
  model_precision, model_recall, model_f1, _ = precision_recall_fscore_support(y_true, y_pred, average="weighted")
  model_results = {"accuracy": model_accuracy,
                  "precision": model_precision,
                  "recall": model_recall,
                  "f1": model_f1}
  return model_results

# Function to evaluate: accuracy, precision, recall, f1-score from sklearn.metrics import accuracy_score, precision_recall_fscore_support def calculate_results(y_true, y_pred): """ Calculates model accuracy, precision, recall and f1 score of a binary classification model. Args: ----- y_true = true labels in the form of a 1D array y_pred = predicted labels in the form of a 1D array Returns a dictionary of accuracy, precision, recall, f1-score. """ # Calculate model accuracy model_accuracy = accuracy_score(y_true, y_pred) * 100 # Calculate model precision, recall and f1 score using "weighted" average model_precision, model_recall, model_f1, _ = precision_recall_fscore_support(y_true, y_pred, average="weighted") model_results = {"accuracy": model_accuracy, "precision": model_precision, "recall": model_recall, "f1": model_f1} return model_results

In [29]:

# Get baseline results
baseline_results = calculate_results(y_true=val_labels,
                                     y_pred=baseline_preds)
baseline_results

# Get baseline results baseline_results = calculate_results(y_true=val_labels, y_pred=baseline_preds) baseline_results

Out[29]:

{'accuracy': 79.26509186351706,
 'precision': 0.8111390004213173,
 'recall': 0.7926509186351706,
 'f1': 0.7862189758049549}

Model 1: A simple dense model¶

The first "deep" model we're going to build is a single layer dense model. In fact, it's barely going to have a single layer.

It'll take our text and labels as input, tokenize the text, create an embedding, find the average of the embedding (using Global Average Pooling) and then pass the average through a fully connected layer with one output unit and a sigmoid activation function.

If the previous sentence sounds like a mouthful, it'll make sense when we code it out (remember, if in doubt, code it out).

And since we're going to be building a number of TensorFlow deep learning models, we'll import our create_tensorboard_callback() function from helper_functions.py to keep track of the results of each.

In [30]:

# Create tensorboard callback (need to create a new one for each model)
from helper_functions import create_tensorboard_callback

# Create directory to save TensorBoard logs
SAVE_DIR = "model_logs"

# Create tensorboard callback (need to create a new one for each model) from helper_functions import create_tensorboard_callback # Create directory to save TensorBoard logs SAVE_DIR = "model_logs"

Now we've got a TensorBoard callback function ready to go, let's build our first deep model.

In [31]:

# Build model with the Functional API
from tensorflow.keras import layers
inputs = layers.Input(shape=(1,), dtype="string") # inputs are 1-dimensional strings
x = text_vectorizer(inputs) # turn the input text into numbers
x = embedding(x) # create an embedding of the numerized numbers
x = layers.GlobalAveragePooling1D()(x) # lower the dimensionality of the embedding (try running the model without this layer and see what happens)
outputs = layers.Dense(1, activation="sigmoid")(x) # create the output layer, want binary outputs so use sigmoid activation
model_1 = tf.keras.Model(inputs, outputs, name="model_1_dense") # construct the model

# Build model with the Functional API from tensorflow.keras import layers inputs = layers.Input(shape=(1,), dtype="string") # inputs are 1-dimensional strings x = text_vectorizer(inputs) # turn the input text into numbers x = embedding(x) # create an embedding of the numerized numbers x = layers.GlobalAveragePooling1D()(x) # lower the dimensionality of the embedding (try running the model without this layer and see what happens) outputs = layers.Dense(1, activation="sigmoid")(x) # create the output layer, want binary outputs so use sigmoid activation model_1 = tf.keras.Model(inputs, outputs, name="model_1_dense") # construct the model

Looking good. Our model takes a 1-dimensional string as input (in our case, a Tweet), it then tokenizes the string using text_vectorizer and creates an embedding using embedding.

We then (optionally) pool the outputs of the embedding layer to reduce the dimensionality of the tensor we pass to the output layer.

🛠 Exercise: Try building model_1 with and without a GlobalAveragePooling1D() layer after the embedding layer. What happens? Why do you think this is?

Finally, we pass the output of the pooling layer to a dense layer with sigmoid activation (we use sigmoid since our problem is binary classification).

Before we can fit our model to the data, we've got to compile it. Since we're working with binary classification, we'll use "binary_crossentropy" as our loss function and the Adam optimizer.

In [32]:

# Compile model
model_1.compile(loss="binary_crossentropy",
                optimizer=tf.keras.optimizers.Adam(),
                metrics=["accuracy"])

# Compile model model_1.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Adam(), metrics=["accuracy"])

Model compiled. Let's get a summary.

In [33]:

# Get a summary of the model
model_1.summary()

# Get a summary of the model model_1.summary()

Model: "model_1_dense"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_1 (InputLayer)        [(None, 1)]               0         
                                                                 
 text_vectorization_1 (TextV  (None, 15)               0         
 ectorization)                                                   
                                                                 
 embedding_1 (Embedding)     (None, 15, 128)           1280000   
                                                                 
 global_average_pooling1d (G  (None, 128)              0         
 lobalAveragePooling1D)                                          
                                                                 
 dense (Dense)               (None, 1)                 129       
                                                                 
=================================================================
Total params: 1,280,129
Trainable params: 1,280,129
Non-trainable params: 0
_________________________________________________________________

Most of the trainable parameters are contained within the embedding layer. Recall we created an embedding of size 128 (output_dim=128) for a vocabulary of size 10,000 (input_dim=10000), hence the 1,280,000 trainable parameters.

Alright, our model is compiled, let's fit it to our training data for 5 epochs. We'll also pass our TensorBoard callback function to make sure our model's training metrics are logged.

In [34]:

# Fit the model
model_1_history = model_1.fit(train_sentences, # input sentences can be a list of strings due to text preprocessing layer built-in model
                              train_labels,
                              epochs=5,
                              validation_data=(val_sentences, val_labels),
                              callbacks=[create_tensorboard_callback(dir_name=SAVE_DIR, 
                                                                     experiment_name="simple_dense_model")])

# Fit the model model_1_history = model_1.fit(train_sentences, # input sentences can be a list of strings due to text preprocessing layer built-in model train_labels, epochs=5, validation_data=(val_sentences, val_labels), callbacks=[create_tensorboard_callback(dir_name=SAVE_DIR, experiment_name="simple_dense_model")])

Saving TensorBoard log files to: model_logs/simple_dense_model/20230526-001451
Epoch 1/5
215/215 [==============================] - 18s 55ms/step - loss: 0.6098 - accuracy: 0.6936 - val_loss: 0.5360 - val_accuracy: 0.7559
Epoch 2/5
215/215 [==============================] - 2s 11ms/step - loss: 0.4417 - accuracy: 0.8194 - val_loss: 0.4691 - val_accuracy: 0.7887
Epoch 3/5
215/215 [==============================] - 2s 10ms/step - loss: 0.3471 - accuracy: 0.8616 - val_loss: 0.4588 - val_accuracy: 0.7887
Epoch 4/5
215/215 [==============================] - 2s 7ms/step - loss: 0.2856 - accuracy: 0.8921 - val_loss: 0.4637 - val_accuracy: 0.7913
Epoch 5/5
215/215 [==============================] - 2s 8ms/step - loss: 0.2388 - accuracy: 0.9115 - val_loss: 0.4760 - val_accuracy: 0.7861

Nice! Since we're using such a simple model, each epoch processes very quickly.

Let's check our model's performance on the validation set.

In [35]:

# Check the results
model_1.evaluate(val_sentences, val_labels)

# Check the results model_1.evaluate(val_sentences, val_labels)

24/24 [==============================] - 0s 2ms/step - loss: 0.4760 - accuracy: 0.7861

Out[35]:

[0.4760194718837738, 0.7860892415046692]

In [36]:

embedding.weights

embedding.weights

Out[36]:

[<tf.Variable 'embedding_1/embeddings:0' shape=(10000, 128) dtype=float32, numpy=
 array([[-0.01078545,  0.05590528,  0.03125916, ..., -0.0312557 ,
         -0.05340781, -0.03800201],
        [-0.02370532,  0.01161508,  0.0097667 , ..., -0.04962142,
         -0.00636482,  0.03781125],
        [-0.05472897,  0.05356752,  0.02146765, ...,  0.05501205,
          0.01705659, -0.05321405],
        ...,
        [ 0.01756669, -0.03676652, -0.00949616, ..., -0.00987446,
         -0.04183743,  0.03016822],
        [-0.07823883,  0.06081628, -0.07657789, ...,  0.07998865,
         -0.05281445, -0.02332675],
        [-0.03393482,  0.08871375, -0.06819566, ...,  0.06992952,
         -0.09992232, -0.02705033]], dtype=float32)>]

In [37]:

embed_weights = model_1.get_layer("embedding_1").get_weights()[0]
print(embed_weights.shape)

embed_weights = model_1.get_layer("embedding_1").get_weights()[0] print(embed_weights.shape)

(10000, 128)

And since we tracked our model's training logs with TensorBoard, how about we visualize them?

We can do so by uploading our TensorBoard log files (contained in the model_logs directory) to TensorBoard.dev.

🔑 Note: Remember, whatever you upload to TensorBoard.dev becomes public. If there are training logs you don't want to share, don't upload them.

In [38]:

# # View tensorboard logs of transfer learning modelling experiments (should be 4 models)
# # Upload TensorBoard dev records
# !tensorboard dev upload --logdir ./model_logs \
#   --name "First deep model on text data" \
#   --description "Trying a dense model with an embedding layer" \
#   --one_shot # exits the uploader when upload has finished

# # View tensorboard logs of transfer learning modelling experiments (should be 4 models) # # Upload TensorBoard dev records # !tensorboard dev upload --logdir ./model_logs \ # --name "First deep model on text data" \ # --description "Trying a dense model with an embedding layer" \ # --one_shot # exits the uploader when upload has finished

In [39]:

# If you need to remove previous experiments, you can do so using the following command
# !tensorboard dev delete --experiment_id EXPERIMENT_ID_TO_DELETE

# If you need to remove previous experiments, you can do so using the following command # !tensorboard dev delete --experiment_id EXPERIMENT_ID_TO_DELETE

The TensorBoard.dev experiment for our first deep model can be viewed here: https://tensorboard.dev/experiment/5d1Xm10aT6m6MgyW3HAGfw/

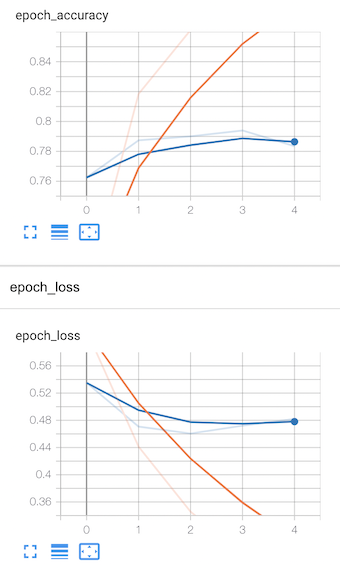
What the training curves of our model look like on TensorBoard. From looking at the curves can you tell if the model is overfitting or underfitting?

Beautiful! Those are some colorful training curves. Would you say the model is overfitting or underfitting?

We've built and trained our first deep model, the next step is to make some predictions with it.

In [40]:

# Make predictions (these come back in the form of probabilities)
model_1_pred_probs = model_1.predict(val_sentences)
model_1_pred_probs[:10] # only print out the first 10 prediction probabilities

# Make predictions (these come back in the form of probabilities) model_1_pred_probs = model_1.predict(val_sentences) model_1_pred_probs[:10] # only print out the first 10 prediction probabilities

24/24 [==============================] - 0s 2ms/step

Out[40]:

array([[0.4068562 ],
       [0.74714756],
       [0.9978309 ],
       [0.10913013],
       [0.10925023],
       [0.93645686],
       [0.91428435],
       [0.99250424],
       [0.96829313],
       [0.26842445]], dtype=float32)

Since our final layer uses a sigmoid activation function, we get our predictions back in the form of probabilities.

To convert them to prediction classes, we'll use tf.round(), meaning prediction probabilities below 0.5 will be rounded to 0 and those above 0.5 will be rounded to 1.

🔑 Note: In practice, the output threshold of a sigmoid prediction probability doesn't necessarily have to 0.5. For example, through testing, you may find that a cut off of 0.25 is better for your chosen evaluation metrics. A common example of this threshold cutoff is the precision-recall tradeoff (search for the keyword "tradeoff" to learn about the phenomenon).

In [41]:

# Turn prediction probabilities into single-dimension tensor of floats
model_1_preds = tf.squeeze(tf.round(model_1_pred_probs)) # squeeze removes single dimensions
model_1_preds[:20]

# Turn prediction probabilities into single-dimension tensor of floats model_1_preds = tf.squeeze(tf.round(model_1_pred_probs)) # squeeze removes single dimensions model_1_preds[:20]

Out[41]:

<tf.Tensor: shape=(20,), dtype=float32, numpy=
array([0., 1., 1., 0., 0., 1., 1., 1., 1., 0., 0., 1., 0., 0., 0., 0., 0.,
       0., 0., 1.], dtype=float32)>

Now we've got our model's predictions in the form of classes, we can use our calculate_results() function to compare them to the ground truth validation labels.

In [42]:

# Calculate model_1 metrics
model_1_results = calculate_results(y_true=val_labels, 
                                    y_pred=model_1_preds)
model_1_results

# Calculate model_1 metrics model_1_results = calculate_results(y_true=val_labels, y_pred=model_1_preds) model_1_results

Out[42]:

{'accuracy': 78.60892388451444,
 'precision': 0.7903277546022673,
 'recall': 0.7860892388451444,
 'f1': 0.7832971347503846}

How about we compare our first deep model to our baseline model?

In [43]:

# Is our simple Keras model better than our baseline model?
import numpy as np
np.array(list(model_1_results.values())) > np.array(list(baseline_results.values()))

# Is our simple Keras model better than our baseline model? import numpy as np np.array(list(model_1_results.values())) > np.array(list(baseline_results.values()))

Out[43]:

array([False, False, False, False])

Since we'll be doing this kind of comparison (baseline compared to new model) quite a few times, let's create a function to help us out.

In [44]:

# Create a helper function to compare our baseline results to new model results
def compare_baseline_to_new_results(baseline_results, new_model_results):
  for key, value in baseline_results.items():
    print(f"Baseline {key}: {value:.2f}, New {key}: {new_model_results[key]:.2f}, Difference: {new_model_results[key]-value:.2f}")

compare_baseline_to_new_results(baseline_results=baseline_results, 
                                new_model_results=model_1_results)

# Create a helper function to compare our baseline results to new model results def compare_baseline_to_new_results(baseline_results, new_model_results): for key, value in baseline_results.items(): print(f"Baseline {key}: {value:.2f}, New {key}: {new_model_results[key]:.2f}, Difference: {new_model_results[key]-value:.2f}") compare_baseline_to_new_results(baseline_results=baseline_results, new_model_results=model_1_results)

Baseline accuracy: 79.27, New accuracy: 78.61, Difference: -0.66
Baseline precision: 0.81, New precision: 0.79, Difference: -0.02
Baseline recall: 0.79, New recall: 0.79, Difference: -0.01
Baseline f1: 0.79, New f1: 0.78, Difference: -0.00

Visualizing learned embeddings¶

Our first model (model_1) contained an embedding layer (embedding) which learned a way of representing words as feature vectors by passing over the training data.

Hearing this for the first few times may sound confusing.

So to further help understand what a text embedding is, let's visualize the embedding our model learned.

To do so, let's remind ourselves of the words in our vocabulary.

In [45]:

# Get the vocabulary from the text vectorization layer
words_in_vocab = text_vectorizer.get_vocabulary()
len(words_in_vocab), words_in_vocab[:10]

# Get the vocabulary from the text vectorization layer words_in_vocab = text_vectorizer.get_vocabulary() len(words_in_vocab), words_in_vocab[:10]

Out[45]:

(10000, ['', '[UNK]', 'the', 'a', 'in', 'to', 'of', 'and', 'i', 'is'])

And now let's get our embedding layer's weights (these are the numerical representations of each word).

In [46]:

model_1.summary()

model_1.summary()

Model: "model_1_dense"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_1 (InputLayer)        [(None, 1)]               0         
                                                                 
 text_vectorization_1 (TextV  (None, 15)               0         
 ectorization)                                                   
                                                                 
 embedding_1 (Embedding)     (None, 15, 128)           1280000   
                                                                 
 global_average_pooling1d (G  (None, 128)              0         
 lobalAveragePooling1D)                                          
                                                                 
 dense (Dense)               (None, 1)                 129       
                                                                 
=================================================================
Total params: 1,280,129
Trainable params: 1,280,129
Non-trainable params: 0
_________________________________________________________________

In [47]:

# Get the weight matrix of embedding layer 
# (these are the numerical patterns between the text in the training dataset the model has learned)
embed_weights = model_1.get_layer("embedding_1").get_weights()[0]
print(embed_weights.shape) # same size as vocab size and embedding_dim (each word is a embedding_dim size vector)

# Get the weight matrix of embedding layer # (these are the numerical patterns between the text in the training dataset the model has learned) embed_weights = model_1.get_layer("embedding_1").get_weights()[0] print(embed_weights.shape) # same size as vocab size and embedding_dim (each word is a embedding_dim size vector)

(10000, 128)

Now we've got these two objects, we can use the Embedding Projector tool to visualize our embedding.

To use the Embedding Projector tool, we need two files:

• The embedding vectors (same as embedding weights).
• The meta data of the embedding vectors (the words they represent - our vocabulary).

Right now, we've got of these files as Python objects. To download them to file, we're going to use the code example available on the TensorFlow word embeddings tutorial page.

In [48]:

# # Code below is adapted from: https://www.tensorflow.org/tutorials/text/word_embeddings#retrieve_the_trained_word_embeddings_and_save_them_to_disk
# import io

# # Create output writers
# out_v = io.open("embedding_vectors.tsv", "w", encoding="utf-8")
# out_m = io.open("embedding_metadata.tsv", "w", encoding="utf-8")

# # Write embedding vectors and words to file
# for num, word in enumerate(words_in_vocab):
#   if num == 0: 
#      continue # skip padding token
#   vec = embed_weights[num]
#   out_m.write(word + "\n") # write words to file
#   out_v.write("\t".join([str(x) for x in vec]) + "\n") # write corresponding word vector to file
# out_v.close()
# out_m.close()

# # Download files locally to upload to Embedding Projector
# try:
#   from google.colab import files
# except ImportError:
#   pass
# else:
#   files.download("embedding_vectors.tsv")
#   files.download("embedding_metadata.tsv")

# # Code below is adapted from: https://www.tensorflow.org/tutorials/text/word_embeddings#retrieve_the_trained_word_embeddings_and_save_them_to_disk # import io # # Create output writers # out_v = io.open("embedding_vectors.tsv", "w", encoding="utf-8") # out_m = io.open("embedding_metadata.tsv", "w", encoding="utf-8") # # Write embedding vectors and words to file # for num, word in enumerate(words_in_vocab): # if num == 0: # continue # skip padding token # vec = embed_weights[num] # out_m.write(word + "\n") # write words to file # out_v.write("\t".join([str(x) for x in vec]) + "\n") # write corresponding word vector to file # out_v.close() # out_m.close() # # Download files locally to upload to Embedding Projector # try: # from google.colab import files # except ImportError: # pass # else: # files.download("embedding_vectors.tsv") # files.download("embedding_metadata.tsv")

Once you've downloaded the embedding vectors and metadata, you can visualize them using Embedding Vector tool:

1. Go to http://projector.tensorflow.org/
2. Click on "Load data"
3. Upload the two files you downloaded (embedding_vectors.tsv and embedding_metadata.tsv)
4. Explore
5. Optional: You can share the data you've created by clicking "Publish"

What do you find?

Are words with similar meanings close together?

Remember, they might not be. The embeddings we downloaded are how our model interprets words, not necessarily how we interpret them.

Also, since the embedding has been learned purely from Tweets, it may contain some strange values as Tweets are a very unique style of natural language.

🤔 Question: Do you have to visualize embeddings every time?

No. Although helpful for gaining an intuition of what natural language embeddings are, it's not completely necessary. Especially as the dimensions of your vocabulary and embeddings grow, trying to comprehend them would become an increasingly difficult task.

Recurrent Neural Networks (RNN's)¶

For our next series of modelling experiments we're going to be using a special kind of neural network called a Recurrent Neural Network (RNN).

The premise of an RNN is simple: use information from the past to help you with the future (this is where the term recurrent comes from). In other words, take an input (X) and compute an output (y) based on all previous inputs.

This concept is especially helpful when dealing with sequences such as passages of natural language text (such as our Tweets).

For example, when you read this sentence, you take into context the previous words when deciphering the meaning of the current word dog.

See what happened there?

I put the word "dog" at the end which is a valid word but it doesn't make sense in the context of the rest of the sentence.

When an RNN looks at a sequence of text (already in numerical form), the patterns it learns are continually updated based on the order of the sequence.

For a simple example, take two sentences:

1. Massive earthquake last week, no?
2. No massive earthquake last week.

Both contain exactly the same words but have different meaning. The order of the words determines the meaning (one could argue punctuation marks also dictate the meaning but for simplicity sake, let's stay focused on the words).

Recurrent neural networks can be used for a number of sequence-based problems:

• One to one: one input, one output, such as image classification.
• One to many: one input, many outputs, such as image captioning (image input, a sequence of text as caption output).
• Many to one: many inputs, one outputs, such as text classification (classifying a Tweet as real diaster or not real diaster).
• Many to many: many inputs, many outputs, such as machine translation (translating English to Spanish) or speech to text (audio wave as input, text as output).

When you come across RNN's in the wild, you'll most likely come across variants of the following:

• Long short-term memory cells (LSTMs).
• Gated recurrent units (GRUs).
• Bidirectional RNN's (passes forward and backward along a sequence, left to right and right to left).

Going into the details of each these is beyond the scope of this notebook (we're going to focus on using them instead), the main thing you should know for now is that they've proven very effective at modelling sequences.

For a deeper understanding of what's happening behind the scenes of the code we're about to write, I'd recommend the following resources:

📖 Resources:

• MIT Deep Learning Lecture on Recurrent Neural Networks - explains the background of recurrent neural networks and introduces LSTMs.
• The Unreasonable Effectiveness of Recurrent Neural Networks by Andrej Karpathy - demonstrates the power of RNN's with examples generating various sequences.
• Understanding LSTMs by Chris Olah - an in-depth (and technical) look at the mechanics of the LSTM cell, possibly the most popular RNN building block.

Model 2: LSTM¶

With all this talk of what RNN's are and what they're good for, I'm sure you're eager to build one.

We're going to start with an LSTM-powered RNN.

To harness the power of the LSTM cell (LSTM cell and LSTM layer are often used interchangably) in TensorFlow, we'll use tensorflow.keras.layers.LSTM().

Coloured block example of the structure of an recurrent neural network.

Our model is going to take on a very similar structure to model_1:

Input (text) -> Tokenize -> Embedding -> Layers -> Output (label probability)

The main difference will be that we're going to add an LSTM layer between our embedding and output.

And to make sure we're not getting reusing trained embeddings (this would involve data leakage between models, leading to an uneven comparison later on), we'll create another embedding layer (model_2_embedding) for our model. The text_vectorizer layer can be reused since it doesn't get updated during training.

🔑 Note: The reason we use a new embedding layer for each model is since the embedding layer is a learned representation of words (as numbers), if we were to use the same embedding layer (embedding_1) for each model, we'd be mixing what one model learned with the next. And because we want to compare our models later on, starting them with their own embedding layer each time is a better idea.

In [49]:

# Set random seed and create embedding layer (new embedding layer for each model)
tf.random.set_seed(42)
from tensorflow.keras import layers
model_2_embedding = layers.Embedding(input_dim=max_vocab_length,
                                     output_dim=128,
                                     embeddings_initializer="uniform",
                                     input_length=max_length,
                                     name="embedding_2")


# Create LSTM model
inputs = layers.Input(shape=(1,), dtype="string")
x = text_vectorizer(inputs)
x = model_2_embedding(x)
print(x.shape)
# x = layers.LSTM(64, return_sequences=True)(x) # return vector for each word in the Tweet (you can stack RNN cells as long as return_sequences=True)
x = layers.LSTM(64)(x) # return vector for whole sequence
print(x.shape)
# x = layers.Dense(64, activation="relu")(x) # optional dense layer on top of output of LSTM cell
outputs = layers.Dense(1, activation="sigmoid")(x)
model_2 = tf.keras.Model(inputs, outputs, name="model_2_LSTM")

# Set random seed and create embedding layer (new embedding layer for each model) tf.random.set_seed(42) from tensorflow.keras import layers model_2_embedding = layers.Embedding(input_dim=max_vocab_length, output_dim=128, embeddings_initializer="uniform", input_length=max_length, name="embedding_2") # Create LSTM model inputs = layers.Input(shape=(1,), dtype="string") x = text_vectorizer(inputs) x = model_2_embedding(x) print(x.shape) # x = layers.LSTM(64, return_sequences=True)(x) # return vector for each word in the Tweet (you can stack RNN cells as long as return_sequences=True) x = layers.LSTM(64)(x) # return vector for whole sequence print(x.shape) # x = layers.Dense(64, activation="relu")(x) # optional dense layer on top of output of LSTM cell outputs = layers.Dense(1, activation="sigmoid")(x) model_2 = tf.keras.Model(inputs, outputs, name="model_2_LSTM")

(None, 15, 128)
(None, 64)

🔑 Note: Reading the documentation for the TensorFlow LSTM layer, you'll find a plethora of parameters. Many of these have been tuned to make sure they compute as fast as possible. The main ones you'll be looking to adjust are units (number of hidden units) and return_sequences (set this to True when stacking LSTM or other recurrent layers).

Now we've got our LSTM model built, let's compile it using "binary_crossentropy" loss and the Adam optimizer.

In [50]:

# Compile model
model_2.compile(loss="binary_crossentropy",
                optimizer=tf.keras.optimizers.Adam(),
                metrics=["accuracy"])

# Compile model model_2.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Adam(), metrics=["accuracy"])

And before we fit our model to the data, let's get a summary.

In [51]:

model_2.summary()

model_2.summary()

Model: "model_2_LSTM"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_2 (InputLayer)        [(None, 1)]               0         
                                                                 
 text_vectorization_1 (TextV  (None, 15)               0         
 ectorization)                                                   
                                                                 
 embedding_2 (Embedding)     (None, 15, 128)           1280000   
                                                                 
 lstm (LSTM)                 (None, 64)                49408     
                                                                 
 dense_1 (Dense)             (None, 1)                 65        
                                                                 
=================================================================
Total params: 1,329,473
Trainable params: 1,329,473
Non-trainable params: 0
_________________________________________________________________

Looking good! You'll notice a fair few more trainable parameters within our LSTM layer than model_1.

If you'd like to know where this number comes from, I recommend going through the above resources as well the following on calculating the number of parameters in an LSTM cell:

• Stack Overflow answer to calculate the number of parameters in an LSTM cell by Marcin Możejko
• Calculating number of parameters in a LSTM unit and layer by Shridhar Priyadarshi

Now our first RNN model's compiled let's fit it to our training data, validating it on the validation data and tracking its training parameters using our TensorBoard callback.

In [52]:

# Fit model
model_2_history = model_2.fit(train_sentences,
                              train_labels,
                              epochs=5,
                              validation_data=(val_sentences, val_labels),
                              callbacks=[create_tensorboard_callback(SAVE_DIR, 
                                                                     "LSTM")])

# Fit model model_2_history = model_2.fit(train_sentences, train_labels, epochs=5, validation_data=(val_sentences, val_labels), callbacks=[create_tensorboard_callback(SAVE_DIR, "LSTM")])

Saving TensorBoard log files to: model_logs/LSTM/20230526-001518
Epoch 1/5
215/215 [==============================] - 13s 44ms/step - loss: 0.5074 - accuracy: 0.7460 - val_loss: 0.4590 - val_accuracy: 0.7743
Epoch 2/5
215/215 [==============================] - 2s 10ms/step - loss: 0.3168 - accuracy: 0.8716 - val_loss: 0.5119 - val_accuracy: 0.7756
Epoch 3/5
215/215 [==============================] - 2s 10ms/step - loss: 0.2198 - accuracy: 0.9155 - val_loss: 0.5876 - val_accuracy: 0.7677
Epoch 4/5
215/215 [==============================] - 2s 8ms/step - loss: 0.1577 - accuracy: 0.9442 - val_loss: 0.5923 - val_accuracy: 0.7795
Epoch 5/5
215/215 [==============================] - 2s 8ms/step - loss: 0.1108 - accuracy: 0.9577 - val_loss: 0.8550 - val_accuracy: 0.7559

Nice! We've got our first trained RNN model using LSTM cells. Let's make some predictions with it.

The same thing will happen as before, due to the sigmoid activiation function in the final layer, when we call the predict() method on our model, it'll return prediction probabilities rather than classes.

In [53]:

# Make predictions on the validation dataset
model_2_pred_probs = model_2.predict(val_sentences)
model_2_pred_probs.shape, model_2_pred_probs[:10] # view the first 10

# Make predictions on the validation dataset model_2_pred_probs = model_2.predict(val_sentences) model_2_pred_probs.shape, model_2_pred_probs[:10] # view the first 10

24/24 [==============================] - 0s 2ms/step

Out[53]:

((762, 1),
 array([[0.00630066],
        [0.7862389 ],
        [0.9991792 ],
        [0.06841089],
        [0.00448257],
        [0.99932086],
        [0.8617405 ],
        [0.99968505],
        [0.9993248 ],
        [0.57989997]], dtype=float32))

We can turn these prediction probabilities into prediction classes by rounding to the nearest integer (by default, prediction probabilities under 0.5 will go to 0 and those over 0.5 will go to 1).

In [54]:

# Round out predictions and reduce to 1-dimensional array
model_2_preds = tf.squeeze(tf.round(model_2_pred_probs))
model_2_preds[:10]

# Round out predictions and reduce to 1-dimensional array model_2_preds = tf.squeeze(tf.round(model_2_pred_probs)) model_2_preds[:10]

Out[54]:

<tf.Tensor: shape=(10,), dtype=float32, numpy=array([0., 1., 1., 0., 0., 1., 1., 1., 1., 1.], dtype=float32)>

Beautiful, now let's use our caculate_results() function to evaluate our LSTM model and our compare_baseline_to_new_results() function to compare it to our baseline model.

In [55]:

# Calculate LSTM model results
model_2_results = calculate_results(y_true=val_labels,
                                    y_pred=model_2_preds)
model_2_results

# Calculate LSTM model results model_2_results = calculate_results(y_true=val_labels, y_pred=model_2_preds) model_2_results

Out[55]:

{'accuracy': 75.59055118110236,
 'precision': 0.7567160722556739,
 'recall': 0.7559055118110236,
 'f1': 0.7539595513230887}

In [56]:

# Compare model 2 to baseline
compare_baseline_to_new_results(baseline_results, model_2_results)

# Compare model 2 to baseline compare_baseline_to_new_results(baseline_results, model_2_results)

Baseline accuracy: 79.27, New accuracy: 75.59, Difference: -3.67
Baseline precision: 0.81, New precision: 0.76, Difference: -0.05
Baseline recall: 0.79, New recall: 0.76, Difference: -0.04
Baseline f1: 0.79, New f1: 0.75, Difference: -0.03

Model 3: GRU¶

Another popular and effective RNN component is the GRU or gated recurrent unit.

The GRU cell has similar features to an LSTM cell but has less parameters.

📖 Resource: A full explanation of the GRU cell is beyond the scope of this noteook but I'd suggest the following resources to learn more:

• Gated Recurrent Unit Wikipedia page
• Understanding GRU networks by Simeon Kostadinov

To use the GRU cell in TensorFlow, we can call the tensorflow.keras.layers.GRU() class.

The architecture of the GRU-powered model will follow the same structure we've been using:

Input (text) -> Tokenize -> Embedding -> Layers -> Output (label probability)

Again, the only difference will be the layer(s) we use between the embedding and the output.

In [57]:

# Set random seed and create embedding layer (new embedding layer for each model)
tf.random.set_seed(42)
from tensorflow.keras import layers
model_3_embedding = layers.Embedding(input_dim=max_vocab_length,
                                     output_dim=128,
                                     embeddings_initializer="uniform",
                                     input_length=max_length,
                                     name="embedding_3")

# Build an RNN using the GRU cell
inputs = layers.Input(shape=(1,), dtype="string")
x = text_vectorizer(inputs)
x = model_3_embedding(x)
# x = layers.GRU(64, return_sequences=True) # stacking recurrent cells requires return_sequences=True
x = layers.GRU(64)(x) 
# x = layers.Dense(64, activation="relu")(x) # optional dense layer after GRU cell
outputs = layers.Dense(1, activation="sigmoid")(x)
model_3 = tf.keras.Model(inputs, outputs, name="model_3_GRU")

# Set random seed and create embedding layer (new embedding layer for each model) tf.random.set_seed(42) from tensorflow.keras import layers model_3_embedding = layers.Embedding(input_dim=max_vocab_length, output_dim=128, embeddings_initializer="uniform", input_length=max_length, name="embedding_3") # Build an RNN using the GRU cell inputs = layers.Input(shape=(1,), dtype="string") x = text_vectorizer(inputs) x = model_3_embedding(x) # x = layers.GRU(64, return_sequences=True) # stacking recurrent cells requires return_sequences=True x = layers.GRU(64)(x) # x = layers.Dense(64, activation="relu")(x) # optional dense layer after GRU cell outputs = layers.Dense(1, activation="sigmoid")(x) model_3 = tf.keras.Model(inputs, outputs, name="model_3_GRU")

TensorFlow makes it easy to use powerful components such as the GRU cell in our models. And now our third model is built, let's compile it, just as before.

In [58]:

# Compile GRU model
model_3.compile(loss="binary_crossentropy",
                optimizer=tf.keras.optimizers.Adam(),
                metrics=["accuracy"])

# Compile GRU model model_3.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Adam(), metrics=["accuracy"])

What does a summary of our model look like?

In [59]:

# Get a summary of the GRU model
model_3.summary()

# Get a summary of the GRU model model_3.summary()

Model: "model_3_GRU"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_3 (InputLayer)        [(None, 1)]               0         
                                                                 
 text_vectorization_1 (TextV  (None, 15)               0         
 ectorization)                                                   
                                                                 
 embedding_3 (Embedding)     (None, 15, 128)           1280000   
                                                                 
 gru (GRU)                   (None, 64)                37248     
                                                                 
 dense_2 (Dense)             (None, 1)                 65        
                                                                 
=================================================================
Total params: 1,317,313
Trainable params: 1,317,313
Non-trainable params: 0
_________________________________________________________________

Notice the difference in number of trainable parameters between model_2 (LSTM) and model_3 (GRU). The difference comes from the LSTM cell having more trainable parameters than the GRU cell.

We'll fit our model just as we've been doing previously. We'll also track our models results using our create_tensorboard_callback() function.

In [60]:

# Fit model
model_3_history = model_3.fit(train_sentences,
                              train_labels,
                              epochs=5,
                              validation_data=(val_sentences, val_labels),
                              callbacks=[create_tensorboard_callback(SAVE_DIR, "GRU")])

# Fit model model_3_history = model_3.fit(train_sentences, train_labels, epochs=5, validation_data=(val_sentences, val_labels), callbacks=[create_tensorboard_callback(SAVE_DIR, "GRU")])

Saving TensorBoard log files to: model_logs/GRU/20230526-001539
Epoch 1/5
215/215 [==============================] - 11s 43ms/step - loss: 0.5274 - accuracy: 0.7231 - val_loss: 0.4539 - val_accuracy: 0.7795
Epoch 2/5
215/215 [==============================] - 2s 10ms/step - loss: 0.3179 - accuracy: 0.8686 - val_loss: 0.4850 - val_accuracy: 0.7848
Epoch 3/5
215/215 [==============================] - 2s 9ms/step - loss: 0.2149 - accuracy: 0.9187 - val_loss: 0.5544 - val_accuracy: 0.7717
Epoch 4/5
215/215 [==============================] - 2s 8ms/step - loss: 0.1517 - accuracy: 0.9488 - val_loss: 0.6279 - val_accuracy: 0.7835
Epoch 5/5
215/215 [==============================] - 2s 8ms/step - loss: 0.1145 - accuracy: 0.9609 - val_loss: 0.6063 - val_accuracy: 0.7756

Due to the optimized default settings of the GRU cell in TensorFlow, training doesn't take long at all.

Time to make some predictions on the validation samples.

In [61]:

# Make predictions on the validation data
model_3_pred_probs = model_3.predict(val_sentences)
model_3_pred_probs.shape, model_3_pred_probs[:10]

# Make predictions on the validation data model_3_pred_probs = model_3.predict(val_sentences) model_3_pred_probs.shape, model_3_pred_probs[:10]

24/24 [==============================] - 0s 2ms/step

Out[61]:

((762, 1),
 array([[0.31703022],
        [0.9160779 ],
        [0.9977792 ],
        [0.14830083],
        [0.01086212],
        [0.9908326 ],
        [0.6938264 ],
        [0.9978917 ],
        [0.99662066],
        [0.4299642 ]], dtype=float32))

Again we get an array of prediction probabilities back which we can convert to prediction classes by rounding them.

In [62]:

# Convert prediction probabilities to prediction classes
model_3_preds = tf.squeeze(tf.round(model_3_pred_probs))
model_3_preds[:10]

# Convert prediction probabilities to prediction classes model_3_preds = tf.squeeze(tf.round(model_3_pred_probs)) model_3_preds[:10]

Out[62]:

<tf.Tensor: shape=(10,), dtype=float32, numpy=array([0., 1., 1., 0., 0., 1., 1., 1., 1., 0.], dtype=float32)>

Now we've got predicted classes, let's evaluate them against the ground truth labels.

In [63]:

# Calcuate model_3 results
model_3_results = calculate_results(y_true=val_labels, 
                                    y_pred=model_3_preds)
model_3_results

# Calcuate model_3 results model_3_results = calculate_results(y_true=val_labels, y_pred=model_3_preds) model_3_results

Out[63]:

{'accuracy': 77.55905511811024,
 'precision': 0.776326889347514,
 'recall': 0.7755905511811023,
 'f1': 0.7740902496040959}

Finally we can compare our GRU model's results to our baseline.

In [64]:

# Compare to baseline
compare_baseline_to_new_results(baseline_results, model_3_results)

# Compare to baseline compare_baseline_to_new_results(baseline_results, model_3_results)

Baseline accuracy: 79.27, New accuracy: 77.56, Difference: -1.71
Baseline precision: 0.81, New precision: 0.78, Difference: -0.03
Baseline recall: 0.79, New recall: 0.78, Difference: -0.02
Baseline f1: 0.79, New f1: 0.77, Difference: -0.01

Model 4: Bidirectonal RNN model¶

Look at us go! We've already built two RNN's with GRU and LSTM cells. Now we're going to look into another kind of RNN, the bidirectional RNN.

A standard RNN will process a sequence from left to right, where as a bidirectional RNN will process the sequence from left to right and then again from right to left.

Intuitively, this can be thought of as if you were reading a sentence for the first time in the normal fashion (left to right) but for some reason it didn't make sense so you traverse back through the words and go back over them again (right to left).

In practice, many sequence models often see and improvement in performance when using bidirectional RNN's.

However, this improvement in performance often comes at the cost of longer training times and increased model parameters (since the model goes left to right and right to left, the number of trainable parameters doubles).

Okay enough talk, let's build a bidirectional RNN.

Once again, TensorFlow helps us out by providing the tensorflow.keras.layers.Bidirectional class. We can use the Bidirectional class to wrap our existing RNNs, instantly making them bidirectional.

In [65]:

# Set random seed and create embedding layer (new embedding layer for each model)
tf.random.set_seed(42)
from tensorflow.keras import layers
model_4_embedding = layers.Embedding(input_dim=max_vocab_length,
                                     output_dim=128,
                                     embeddings_initializer="uniform",
                                     input_length=max_length,
                                     name="embedding_4")

# Build a Bidirectional RNN in TensorFlow
inputs = layers.Input(shape=(1,), dtype="string")
x = text_vectorizer(inputs)
x = model_4_embedding(x)
# x = layers.Bidirectional(layers.LSTM(64, return_sequences=True))(x) # stacking RNN layers requires return_sequences=True
x = layers.Bidirectional(layers.LSTM(64))(x) # bidirectional goes both ways so has double the parameters of a regular LSTM layer
outputs = layers.Dense(1, activation="sigmoid")(x)
model_4 = tf.keras.Model(inputs, outputs, name="model_4_Bidirectional")

# Set random seed and create embedding layer (new embedding layer for each model) tf.random.set_seed(42) from tensorflow.keras import layers model_4_embedding = layers.Embedding(input_dim=max_vocab_length, output_dim=128, embeddings_initializer="uniform", input_length=max_length, name="embedding_4") # Build a Bidirectional RNN in TensorFlow inputs = layers.Input(shape=(1,), dtype="string") x = text_vectorizer(inputs) x = model_4_embedding(x) # x = layers.Bidirectional(layers.LSTM(64, return_sequences=True))(x) # stacking RNN layers requires return_sequences=True x = layers.Bidirectional(layers.LSTM(64))(x) # bidirectional goes both ways so has double the parameters of a regular LSTM layer outputs = layers.Dense(1, activation="sigmoid")(x) model_4 = tf.keras.Model(inputs, outputs, name="model_4_Bidirectional")

🔑 Note: You can use the Bidirectional wrapper on any RNN cell in TensorFlow. For example, layers.Bidirectional(layers.GRU(64)) creates a bidirectional GRU cell.

Our bidirectional model is built, let's compile it.

In [66]:

# Compile
model_4.compile(loss="binary_crossentropy",
                optimizer=tf.keras.optimizers.Adam(),
                metrics=["accuracy"])

# Compile model_4.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Adam(), metrics=["accuracy"])

And of course, we'll check out a summary.

In [67]:

# Get a summary of our bidirectional model
model_4.summary()

# Get a summary of our bidirectional model model_4.summary()

Model: "model_4_Bidirectional"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_4 (InputLayer)        [(None, 1)]               0         
                                                                 
 text_vectorization_1 (TextV  (None, 15)               0         
 ectorization)                                                   
                                                                 
 embedding_4 (Embedding)     (None, 15, 128)           1280000   
                                                                 
 bidirectional (Bidirectiona  (None, 128)              98816     
 l)                                                              
                                                                 
 dense_3 (Dense)             (None, 1)                 129       
                                                                 
=================================================================
Total params: 1,378,945
Trainable params: 1,378,945
Non-trainable params: 0
_________________________________________________________________

Notice the increased number of trainable parameters in model_4 (bidirectional LSTM) compared to model_2 (regular LSTM). This is due to the bidirectionality we added to our RNN.

Time to fit our bidirectional model and track its performance.

In [68]:

# Fit the model (takes longer because of the bidirectional layers)
model_4_history = model_4.fit(train_sentences,
                              train_labels,
                              epochs=5,
                              validation_data=(val_sentences, val_labels),
                              callbacks=[create_tensorboard_callback(SAVE_DIR, "bidirectional_RNN")])

# Fit the model (takes longer because of the bidirectional layers) model_4_history = model_4.fit(train_sentences, train_labels, epochs=5, validation_data=(val_sentences, val_labels), callbacks=[create_tensorboard_callback(SAVE_DIR, "bidirectional_RNN")])

Saving TensorBoard log files to: model_logs/bidirectional_RNN/20230526-001559
Epoch 1/5
215/215 [==============================] - 14s 47ms/step - loss: 0.5096 - accuracy: 0.7447 - val_loss: 0.4585 - val_accuracy: 0.7861
Epoch 2/5
215/215 [==============================] - 2s 12ms/step - loss: 0.3140 - accuracy: 0.8726 - val_loss: 0.5086 - val_accuracy: 0.7743
Epoch 3/5
215/215 [==============================] - 2s 11ms/step - loss: 0.2139 - accuracy: 0.9183 - val_loss: 0.5716 - val_accuracy: 0.7730
Epoch 4/5
215/215 [==============================] - 2s 9ms/step - loss: 0.1486 - accuracy: 0.9504 - val_loss: 0.6707 - val_accuracy: 0.7703
Epoch 5/5
215/215 [==============================] - 2s 10ms/step - loss: 0.1058 - accuracy: 0.9648 - val_loss: 0.6658 - val_accuracy: 0.7677

Due to the bidirectionality of our model we see a slight increase in training time.

Not to worry, it's not too dramatic of an increase.

Let's make some predictions with it.

In [69]:

# Make predictions with bidirectional RNN on the validation data
model_4_pred_probs = model_4.predict(val_sentences)
model_4_pred_probs[:10]

# Make predictions with bidirectional RNN on the validation data model_4_pred_probs = model_4.predict(val_sentences) model_4_pred_probs[:10]

24/24 [==============================] - 1s 3ms/step

Out[69]:

array([[0.05258294],
       [0.8495521 ],
       [0.99898857],
       [0.15441437],
       [0.00566462],
       [0.99576193],
       [0.952807  ],
       [0.9993511 ],
       [0.99936384],
       [0.19425693]], dtype=float32)

And we'll convert them to prediction classes and evaluate them against the ground truth labels and baseline model.

In [70]:

# Convert prediction probabilities to labels
model_4_preds = tf.squeeze(tf.round(model_4_pred_probs))
model_4_preds[:10]

# Convert prediction probabilities to labels model_4_preds = tf.squeeze(tf.round(model_4_pred_probs)) model_4_preds[:10]

Out[70]:

<tf.Tensor: shape=(10,), dtype=float32, numpy=array([0., 1., 1., 0., 0., 1., 1., 1., 1., 0.], dtype=float32)>

In [71]:

# Calculate bidirectional RNN model results
model_4_results = calculate_results(val_labels, model_4_preds)
model_4_results

# Calculate bidirectional RNN model results model_4_results = calculate_results(val_labels, model_4_preds) model_4_results

Out[71]:

{'accuracy': 76.77165354330708,
 'precision': 0.7675450859410361,
 'recall': 0.7677165354330708,
 'f1': 0.7667932666650168}

In [72]:

# Check to see how the bidirectional model performs against the baseline
compare_baseline_to_new_results(baseline_results, model_4_results)

# Check to see how the bidirectional model performs against the baseline compare_baseline_to_new_results(baseline_results, model_4_results)

Baseline accuracy: 79.27, New accuracy: 76.77, Difference: -2.49
Baseline precision: 0.81, New precision: 0.77, Difference: -0.04
Baseline recall: 0.79, New recall: 0.77, Difference: -0.02
Baseline f1: 0.79, New f1: 0.77, Difference: -0.02

Convolutional Neural Networks for Text¶

You might've used convolutional neural networks (CNNs) for images before but they can also be used for sequences.

The main difference between using CNNs for images and sequences is the shape of the data. Images come in 2-dimensions (height x width) where as sequences are often 1-dimensional (a string of text).

So to use CNNs with sequences, we use a 1-dimensional convolution instead of a 2-dimensional convolution.

A typical CNN architecture for sequences will look like the following:

Inputs (text) -> Tokenization -> Embedding -> Layers -> Outputs (class probabilities)

You might be thinking "that just looks like the architecture layout we've been using for the other models..."

And you'd be right.

The difference again is in the layers component. Instead of using an LSTM or GRU cell, we're going to use a tensorflow.keras.layers.Conv1D() layer followed by a tensorflow.keras.layers.GlobablMaxPool1D() layer.

1. 1-dimensional convolving filters are used as ngram detectors, each filter specializing in a closely-related family of ngrams (an ngram is a collection of n-words, for example, an ngram of 5 might result in "hello, my name is Daniel").
2. Max-pooling over time extracts the relevant ngrams for making a decision.
3. The rest of the network classifies the text based on this information.

📖 Resource: The intuition here is explained succinctly in the paper Understanding Convolutional Neural Networks for Text Classification, where they state that CNNs classify text through the following steps:

Model 5: Conv1D¶

Before we build a full 1-dimensional CNN model, let's see a 1-dimensional convolutional layer (also called a temporal convolution) in action.

We'll first create an embedding of a sample of text and experiment passing it through a Conv1D() layer and GlobalMaxPool1D() layer.

In [73]:

# Test out the embedding, 1D convolutional and max pooling
embedding_test = embedding(text_vectorizer(["this is a test sentence"])) # turn target sentence into embedding
conv_1d = layers.Conv1D(filters=32, kernel_size=5, activation="relu") # convolve over target sequence 5 words at a time
conv_1d_output = conv_1d(embedding_test) # pass embedding through 1D convolutional layer
max_pool = layers.GlobalMaxPool1D() 
max_pool_output = max_pool(conv_1d_output) # get the most important features
embedding_test.shape, conv_1d_output.shape, max_pool_output.shape

# Test out the embedding, 1D convolutional and max pooling embedding_test = embedding(text_vectorizer(["this is a test sentence"])) # turn target sentence into embedding conv_1d = layers.Conv1D(filters=32, kernel_size=5, activation="relu") # convolve over target sequence 5 words at a time conv_1d_output = conv_1d(embedding_test) # pass embedding through 1D convolutional layer max_pool = layers.GlobalMaxPool1D() max_pool_output = max_pool(conv_1d_output) # get the most important features embedding_test.shape, conv_1d_output.shape, max_pool_output.shape

Out[73]:

(TensorShape([1, 15, 128]), TensorShape([1, 11, 32]), TensorShape([1, 32]))

Notice the output shapes of each layer.

The embedding has an output shape dimension of the parameters we set it to (input_length=15 and output_dim=128).

The 1-dimensional convolutional layer has an output which has been compressed inline with its parameters. And the same goes for the max pooling layer output.

Our text starts out as a string but gets converted to a feature vector of length 64 through various transformation steps (from tokenization to embedding to 1-dimensional convolution to max pool).

Let's take a peak at what each of these transformations looks like.

In [74]:

# See the outputs of each layer
embedding_test[:1], conv_1d_output[:1], max_pool_output[:1]

# See the outputs of each layer embedding_test[:1], conv_1d_output[:1], max_pool_output[:1]

Out[74]:

(<tf.Tensor: shape=(1, 15, 128), dtype=float32, numpy=
 array([[[ 0.01675646, -0.03352517,  0.04817378, ..., -0.02946043,
          -0.03770737,  0.01220698],
         [-0.00607298,  0.06020833, -0.05641982, ...,  0.08325578,
          -0.01878556, -0.08398241],
         [-0.0362346 ,  0.00904451, -0.03833614, ...,  0.0051756 ,
          -0.00220015, -0.0017492 ],
         ...,
         [-0.01078545,  0.05590528,  0.03125916, ..., -0.0312557 ,
          -0.05340781, -0.03800201],
         [-0.01078545,  0.05590528,  0.03125916, ..., -0.0312557 ,
          -0.05340781, -0.03800201],
         [-0.01078545,  0.05590528,  0.03125916, ..., -0.0312557 ,
          -0.05340781, -0.03800201]]], dtype=float32)>,
 <tf.Tensor: shape=(1, 11, 32), dtype=float32, numpy=
 array([[[0.        , 0.10975833, 0.        , 0.        , 0.        ,
          0.06834612, 0.        , 0.02298634, 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.        , 0.06889185,
          0.08162662, 0.        , 0.        , 0.03804683, 0.        ,
          0.        , 0.        , 0.        , 0.00810859, 0.02383356,
          0.        , 0.00385817, 0.        , 0.01310921, 0.        ,
          0.        , 0.16110645],
         [0.05000008, 0.        , 0.03852113, 0.0149918 , 0.03014192,
          0.04613257, 0.        , 0.        , 0.        , 0.05233994,
          0.        , 0.        , 0.07095916, 0.03590994, 0.        ,
          0.        , 0.        , 0.        , 0.        , 0.05599808,
          0.04344876, 0.04021783, 0.        , 0.06110618, 0.        ,
          0.        , 0.        , 0.00198402, 0.        , 0.03175152,
          0.        , 0.04452901],
         [0.        , 0.05068349, 0.06747732, 0.        , 0.        ,
          0.04893802, 0.        , 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.0853087 , 0.01114925, 0.00223987,
          0.        , 0.        , 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.10797694, 0.02317763,
          0.        , 0.01130794, 0.        , 0.01777459, 0.        ,
          0.        , 0.02142338],
         [0.        , 0.01030538, 0.        , 0.        , 0.02127263,
          0.06377578, 0.        , 0.        , 0.        , 0.        ,
          0.03660904, 0.        , 0.13293687, 0.06086106, 0.        ,
          0.        , 0.        , 0.03161986, 0.00114628, 0.02163697,
          0.        , 0.        , 0.        , 0.04408561, 0.        ,
          0.01193662, 0.        , 0.        , 0.01174912, 0.03890226,
          0.        , 0.06139129],
         [0.        , 0.        , 0.00959204, 0.        , 0.03472092,
          0.03202822, 0.        , 0.        , 0.        , 0.        ,
          0.00390257, 0.        , 0.07451484, 0.00349154, 0.        ,
          0.        , 0.02155435, 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.09407972, 0.        ,
          0.        , 0.00077316, 0.        , 0.        , 0.        ,
          0.        , 0.06074456],
         [0.        , 0.03225943, 0.01736662, 0.        , 0.01197381,
          0.02301392, 0.        , 0.        , 0.        , 0.00205472,
          0.02762672, 0.        , 0.06565619, 0.00253076, 0.        ,
          0.        , 0.00745697, 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.09595221, 0.        ,
          0.        , 0.        , 0.        , 0.01910873, 0.        ,
          0.        , 0.06507206],
         [0.        , 0.03225943, 0.01736662, 0.        , 0.01197381,
          0.02301392, 0.        , 0.        , 0.        , 0.00205472,
          0.02762672, 0.        , 0.06565619, 0.00253076, 0.        ,
          0.        , 0.00745697, 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.09595221, 0.        ,
          0.        , 0.        , 0.        , 0.01910873, 0.        ,
          0.        , 0.06507206],
         [0.        , 0.03225943, 0.01736662, 0.        , 0.01197381,
          0.02301392, 0.        , 0.        , 0.        , 0.00205472,
          0.02762672, 0.        , 0.06565619, 0.00253076, 0.        ,
          0.        , 0.00745697, 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.09595221, 0.        ,
          0.        , 0.        , 0.        , 0.01910873, 0.        ,
          0.        , 0.06507206],
         [0.        , 0.03225943, 0.01736662, 0.        , 0.01197381,
          0.02301392, 0.        , 0.        , 0.        , 0.00205472,
          0.02762672, 0.        , 0.06565619, 0.00253076, 0.        ,
          0.        , 0.00745697, 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.09595221, 0.        ,
          0.        , 0.        , 0.        , 0.01910873, 0.        ,
          0.        , 0.06507206],
         [0.        , 0.03225943, 0.01736662, 0.        , 0.01197381,
          0.02301392, 0.        , 0.        , 0.        , 0.00205472,
          0.02762672, 0.        , 0.06565619, 0.00253076, 0.        ,
          0.        , 0.00745697, 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.09595221, 0.        ,
          0.        , 0.        , 0.        , 0.01910873, 0.        ,
          0.        , 0.06507206],
         [0.        , 0.03225943, 0.01736662, 0.        , 0.01197381,
          0.02301392, 0.        , 0.        , 0.        , 0.00205472,
          0.02762672, 0.        , 0.06565619, 0.00253076, 0.        ,
          0.        , 0.00745697, 0.        , 0.        , 0.        ,
          0.        , 0.        , 0.        , 0.09595221, 0.        ,
          0.        , 0.        , 0.        , 0.01910873, 0.        ,
          0.        , 0.06507206]]], dtype=float32)>,
 <tf.Tensor: shape=(1, 32), dtype=float32, numpy=
 array([[0.05000008, 0.10975833, 0.06747732, 0.0149918 , 0.03472092,
         0.06834612, 0.        , 0.02298634, 0.        , 0.05233994,
         0.03660904, 0.        , 0.13293687, 0.06086106, 0.06889185,
         0.08162662, 0.02155435, 0.03161986, 0.03804683, 0.05599808,
         0.04344876, 0.04021783, 0.        , 0.10797694, 0.02383356,
         0.01193662, 0.01130794, 0.00198402, 0.01910873, 0.03890226,
         0.        , 0.16110645]], dtype=float32)>)

Alright, we've seen the outputs of several components of a CNN for sequences, let's put them together and construct a full model, compile it (just as we've done with our other models) and get a summary.

In [75]:

# Set random seed and create embedding layer (new embedding layer for each model)
tf.random.set_seed(42)
from tensorflow.keras import layers
model_5_embedding = layers.Embedding(input_dim=max_vocab_length,
                                     output_dim=128,
                                     embeddings_initializer="uniform",
                                     input_length=max_length,
                                     name="embedding_5")

# Create 1-dimensional convolutional layer to model sequences
from tensorflow.keras import layers
inputs = layers.Input(shape=(1,), dtype="string")
x = text_vectorizer(inputs)
x = model_5_embedding(x)
x = layers.Conv1D(filters=32, kernel_size=5, activation="relu")(x)
x = layers.GlobalMaxPool1D()(x)
# x = layers.Dense(64, activation="relu")(x) # optional dense layer
outputs = layers.Dense(1, activation="sigmoid")(x)
model_5 = tf.keras.Model(inputs, outputs, name="model_5_Conv1D")

# Compile Conv1D model
model_5.compile(loss="binary_crossentropy",
                optimizer=tf.keras.optimizers.Adam(),
                metrics=["accuracy"])

# Get a summary of our 1D convolution model
model_5.summary()

# Set random seed and create embedding layer (new embedding layer for each model) tf.random.set_seed(42) from tensorflow.keras import layers model_5_embedding = layers.Embedding(input_dim=max_vocab_length, output_dim=128, embeddings_initializer="uniform", input_length=max_length, name="embedding_5") # Create 1-dimensional convolutional layer to model sequences from tensorflow.keras import layers inputs = layers.Input(shape=(1,), dtype="string") x = text_vectorizer(inputs) x = model_5_embedding(x) x = layers.Conv1D(filters=32, kernel_size=5, activation="relu")(x) x = layers.GlobalMaxPool1D()(x) # x = layers.Dense(64, activation="relu")(x) # optional dense layer outputs = layers.Dense(1, activation="sigmoid")(x) model_5 = tf.keras.Model(inputs, outputs, name="model_5_Conv1D") # Compile Conv1D model model_5.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Adam(), metrics=["accuracy"]) # Get a summary of our 1D convolution model model_5.summary()

Model: "model_5_Conv1D"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_5 (InputLayer)        [(None, 1)]               0         
                                                                 
 text_vectorization_1 (TextV  (None, 15)               0         
 ectorization)                                                   
                                                                 
 embedding_5 (Embedding)     (None, 15, 128)           1280000   
                                                                 
 conv1d_1 (Conv1D)           (None, 11, 32)            20512     
                                                                 
 global_max_pooling1d_1 (Glo  (None, 32)               0         
 balMaxPooling1D)                                                
                                                                 
 dense_4 (Dense)             (None, 1)                 33        
                                                                 
=================================================================
Total params: 1,300,545
Trainable params: 1,300,545
Non-trainable params: 0
_________________________________________________________________

Woohoo! Looking great! Notice how the number of trainable parameters for the 1-dimensional convolutional layer is similar to that of the LSTM layer in model_2.

Let's fit our 1D CNN model to our text data. In line with previous experiments, we'll save its results using our create_tensorboard_callback() function.

In [76]:

# Fit the model
model_5_history = model_5.fit(train_sentences,
                              train_labels,
                              epochs=5,
                              validation_data=(val_sentences, val_labels),
                              callbacks=[create_tensorboard_callback(SAVE_DIR, 
                                                                     "Conv1D")])

# Fit the model model_5_history = model_5.fit(train_sentences, train_labels, epochs=5, validation_data=(val_sentences, val_labels), callbacks=[create_tensorboard_callback(SAVE_DIR, "Conv1D")])

Saving TensorBoard log files to: model_logs/Conv1D/20230526-001626
Epoch 1/5
215/215 [==============================] - 11s 42ms/step - loss: 0.5693 - accuracy: 0.7108 - val_loss: 0.4736 - val_accuracy: 0.7769
Epoch 2/5
215/215 [==============================] - 2s 9ms/step - loss: 0.3426 - accuracy: 0.8600 - val_loss: 0.4677 - val_accuracy: 0.7874
Epoch 3/5
215/215 [==============================] - 2s 9ms/step - loss: 0.2130 - accuracy: 0.9202 - val_loss: 0.5374 - val_accuracy: 0.7677
Epoch 4/5
215/215 [==============================] - 1s 7ms/step - loss: 0.1366 - accuracy: 0.9564 - val_loss: 0.6076 - val_accuracy: 0.7756
Epoch 5/5
215/215 [==============================] - 2s 7ms/step - loss: 0.0958 - accuracy: 0.9667 - val_loss: 0.6706 - val_accuracy: 0.7874

Nice! Thanks to GPU acceleration, our 1D convolutional model trains nice and fast. Let's make some predictions with it and evaluate them just as before.

In [77]:

# Make predictions with model_5
model_5_pred_probs = model_5.predict(val_sentences)
model_5_pred_probs[:10]

# Make predictions with model_5 model_5_pred_probs = model_5.predict(val_sentences) model_5_pred_probs[:10]

24/24 [==============================] - 0s 2ms/step

Out[77]:

array([[0.7295443 ],
       [0.63939744],
       [0.9997949 ],
       [0.05865377],
       [0.0070557 ],
       [0.99556965],
       [0.90180606],
       [0.9973731 ],
       [0.99953437],
       [0.6327795 ]], dtype=float32)

In [78]:

# Convert model_5 prediction probabilities to labels
model_5_preds = tf.squeeze(tf.round(model_5_pred_probs))
model_5_preds[:10]

# Convert model_5 prediction probabilities to labels model_5_preds = tf.squeeze(tf.round(model_5_pred_probs)) model_5_preds[:10]

Out[78]:

<tf.Tensor: shape=(10,), dtype=float32, numpy=array([1., 1., 1., 0., 0., 1., 1., 1., 1., 1.], dtype=float32)>

In [79]:

# Calculate model_5 evaluation metrics 
model_5_results = calculate_results(y_true=val_labels, 
                                    y_pred=model_5_preds)
model_5_results

# Calculate model_5 evaluation metrics model_5_results = calculate_results(y_true=val_labels, y_pred=model_5_preds) model_5_results

Out[79]:

{'accuracy': 78.74015748031496,
 'precision': 0.7900609457201325,
 'recall': 0.7874015748031497,
 'f1': 0.7852275674790494}

In [80]:

# Compare model_5 results to baseline 
compare_baseline_to_new_results(baseline_results, model_5_results)

# Compare model_5 results to baseline compare_baseline_to_new_results(baseline_results, model_5_results)

Baseline accuracy: 79.27, New accuracy: 78.74, Difference: -0.52
Baseline precision: 0.81, New precision: 0.79, Difference: -0.02
Baseline recall: 0.79, New recall: 0.79, Difference: -0.01
Baseline f1: 0.79, New f1: 0.79, Difference: -0.00

Using Pretrained Embeddings (transfer learning for NLP)¶

For all of the previous deep learning models we've built and trained, we've created and used our own embeddings from scratch each time.

However, a common practice is to leverage pretrained embeddings through transfer learning. This is one of the main benefits of using deep models: being able to take what one (often larger) model has learned (often on a large amount of data) and adjust it for our own use case.

For our next model, instead of using our own embedding layer, we're going to replace it with a pretrained embedding layer.

More specifically, we're going to be using the Universal Sentence Encoder from TensorFlow Hub (a great resource containing a plethora of pretrained model resources for a variety of tasks).

🔑 Note: There are many different pretrained text embedding options on TensorFlow Hub, however, some require different levels of text preprocessing than others. Best to experiment with a few and see which best suits your use case.

Model 6: TensorFlow Hub Pretrained Sentence Encoder¶

The main difference between the embedding layer we created and the Universal Sentence Encoder is that rather than create a word-level embedding, the Universal Sentence Encoder, as you might've guessed, creates a whole sentence-level embedding.

Our embedding layer also outputs an a 128 dimensional vector for each word, where as, the Universal Sentence Encoder outputs a 512 dimensional vector for each sentence.

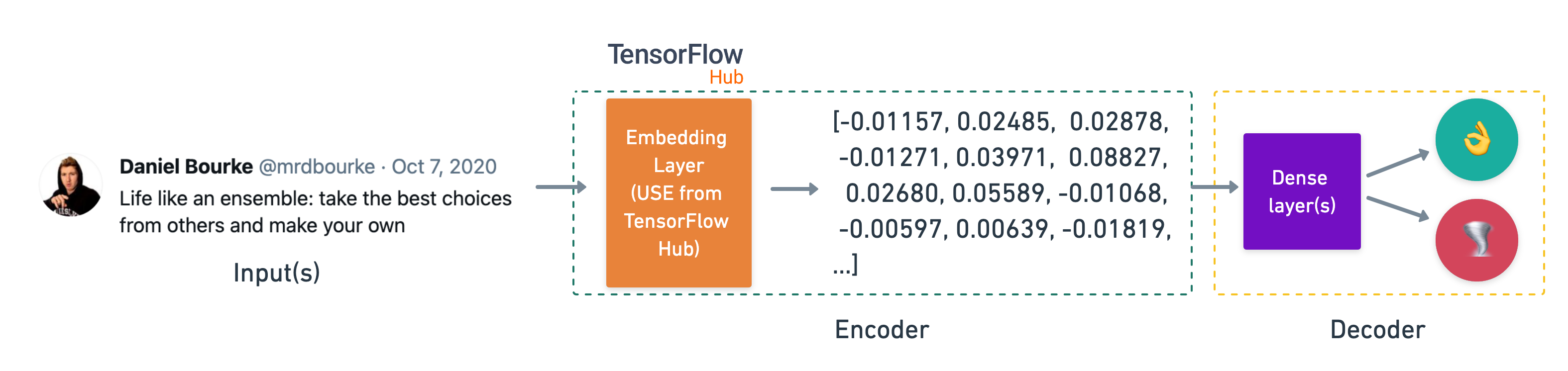The feature extractor model we're building through the eyes of an encoder/decoder model.

🔑 Note: An encoder is the name for a model which converts raw data such as text into a numerical representation (feature vector), a decoder converts the numerical representation to a desired output.

As usual, this is best demonstrated with an example.

We can load in a TensorFlow Hub module using the hub.load() method and passing it the target URL of the module we'd like to use, in our case, it's "https://tfhub.dev/google/universal-sentence-encoder/4".

Let's load the Universal Sentence Encoder model and test it on a couple of sentences.

In [81]:

# Example of pretrained embedding with universal sentence encoder - https://tfhub.dev/google/universal-sentence-encoder/4
import tensorflow_hub as hub
embed = hub.load("https://tfhub.dev/google/universal-sentence-encoder/4") # load Universal Sentence Encoder
embed_samples = embed([sample_sentence,
                      "When you call the universal sentence encoder on a sentence, it turns it into numbers."])

print(embed_samples[0][:50])

# Example of pretrained embedding with universal sentence encoder - https://tfhub.dev/google/universal-sentence-encoder/4 import tensorflow_hub as hub embed = hub.load("https://tfhub.dev/google/universal-sentence-encoder/4") # load Universal Sentence Encoder embed_samples = embed([sample_sentence, "When you call the universal sentence encoder on a sentence, it turns it into numbers."]) print(embed_samples[0][:50])

tf.Tensor(
[-0.01154496  0.02487099  0.0287963  -0.01272263  0.03969951  0.08829075
  0.02682647  0.05582222 -0.01078761 -0.00596655  0.00640638 -0.01816132
  0.0002885   0.09106605  0.05874373 -0.03175148  0.01510153 -0.05164852
  0.0099434  -0.06867751 -0.04210396  0.0267539   0.03008907  0.00320448
 -0.00336865 -0.04790529  0.02267517 -0.00984557 -0.04066692 -0.01285528
 -0.04665243  0.05630673 -0.03952145  0.00521895  0.02495948 -0.07011835
  0.02873133  0.04945794 -0.00634555 -0.08959357  0.02807156 -0.00809173
 -0.01363956  0.05998395 -0.1036155  -0.05192674  0.00232459 -0.02326531
 -0.03752431  0.0333298 ], shape=(50,), dtype=float32)

In [82]:

# Each sentence has been encoded into a 512 dimension vector
embed_samples[0].shape

# Each sentence has been encoded into a 512 dimension vector embed_samples[0].shape

Out[82]:

TensorShape([512])

Passing our sentences to the Universal Sentence Encoder (USE) encodes them from strings to 512 dimensional vectors, which make no sense to us but hopefully make sense to our machine learning models.

Speaking of models, let's build one with the USE as our embedding layer.

We can convert the TensorFlow Hub USE module into a Keras layer using the hub.KerasLayer class.

🔑 Note: Due to the size of the USE TensorFlow Hub module, it may take a little while to download. Once it's downloaded though, it'll be cached and ready to use. And as with many TensorFlow Hub modules, there is a "lite" version of the USE which takes up less space but sacrifices some performance and requires more preprocessing steps. However, depending on your available compute power, the lite version may be better for your application use case.

In [83]:

# We can use this encoding layer in place of our text_vectorizer and embedding layer
sentence_encoder_layer = hub.KerasLayer("https://tfhub.dev/google/universal-sentence-encoder/4",
                                        input_shape=[], # shape of inputs coming to our model 
                                        dtype=tf.string, # data type of inputs coming to the USE layer
                                        trainable=False, # keep the pretrained weights (we'll create a feature extractor)
                                        name="USE")

# We can use this encoding layer in place of our text_vectorizer and embedding layer sentence_encoder_layer = hub.KerasLayer("https://tfhub.dev/google/universal-sentence-encoder/4", input_shape=[], # shape of inputs coming to our model dtype=tf.string, # data type of inputs coming to the USE layer trainable=False, # keep the pretrained weights (we'll create a feature extractor) name="USE")

Beautiful! Now we've got the USE as a Keras layer, we can use it in a Keras Sequential model.

In [84]:

# Create model using the Sequential API
model_6 = tf.keras.Sequential([
  sentence_encoder_layer, # take in sentences and then encode them into an embedding
  layers.Dense(64, activation="relu"),
  layers.Dense(1, activation="sigmoid")
], name="model_6_USE")

# Compile model
model_6.compile(loss="binary_crossentropy",
                optimizer=tf.keras.optimizers.Adam(),
                metrics=["accuracy"])

model_6.summary()

# Create model using the Sequential API model_6 = tf.keras.Sequential([ sentence_encoder_layer, # take in sentences and then encode them into an embedding layers.Dense(64, activation="relu"), layers.Dense(1, activation="sigmoid") ], name="model_6_USE") # Compile model model_6.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Adam(), metrics=["accuracy"]) model_6.summary()

Model: "model_6_USE"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 USE (KerasLayer)            (None, 512)               256797824 
                                                                 
 dense_5 (Dense)             (None, 64)                32832     
                                                                 
 dense_6 (Dense)             (None, 1)                 65        
                                                                 
=================================================================
Total params: 256,830,721
Trainable params: 32,897
Non-trainable params: 256,797,824
_________________________________________________________________

Notice the number of paramters in the USE layer, these are the pretrained weights its learned on various text sources (Wikipedia, web news, web question-answer forums, etc, see the Universal Sentence Encoder paper for more).

The trainable parameters are only in our output layers, in other words, we're keeping the USE weights frozen and using it as a feature-extractor. We could fine-tune these weights by setting trainable=True when creating the hub.KerasLayer instance.

Now we've got a feature extractor model ready, let's train it and track its results to TensorBoard using our create_tensorboard_callback() function.

In [85]:

# Train a classifier on top of pretrained embeddings
model_6_history = model_6.fit(train_sentences,
                              train_labels,
                              epochs=5,
                              validation_data=(val_sentences, val_labels),
                              callbacks=[create_tensorboard_callback(SAVE_DIR, 
                                                                     "tf_hub_sentence_encoder")])

# Train a classifier on top of pretrained embeddings model_6_history = model_6.fit(train_sentences, train_labels, epochs=5, validation_data=(val_sentences, val_labels), callbacks=[create_tensorboard_callback(SAVE_DIR, "tf_hub_sentence_encoder")])

Saving TensorBoard log files to: model_logs/tf_hub_sentence_encoder/20230526-001739
Epoch 1/5
215/215 [==============================] - 6s 11ms/step - loss: 0.5014 - accuracy: 0.7870 - val_loss: 0.4469 - val_accuracy: 0.7992
Epoch 2/5
215/215 [==============================] - 2s 9ms/step - loss: 0.4145 - accuracy: 0.8140 - val_loss: 0.4359 - val_accuracy: 0.8097
Epoch 3/5
215/215 [==============================] - 2s 9ms/step - loss: 0.4000 - accuracy: 0.8216 - val_loss: 0.4319 - val_accuracy: 0.8163
Epoch 4/5
215/215 [==============================] - 2s 9ms/step - loss: 0.3927 - accuracy: 0.8262 - val_loss: 0.4280 - val_accuracy: 0.8176
Epoch 5/5
215/215 [==============================] - 2s 9ms/step - loss: 0.3862 - accuracy: 0.8288 - val_loss: 0.4299 - val_accuracy: 0.8176

USE model trained! Let's make some predictions with it an evaluate them as we've done with our other models.

In [86]:

# Make predictions with USE TF Hub model
model_6_pred_probs = model_6.predict(val_sentences)
model_6_pred_probs[:10]

# Make predictions with USE TF Hub model model_6_pred_probs = model_6.predict(val_sentences) model_6_pred_probs[:10]

24/24 [==============================] - 1s 7ms/step

Out[86]:

array([[0.14814094],
       [0.74057853],
       [0.9886474 ],
       [0.22455953],
       [0.7404941 ],
       [0.6678845 ],
       [0.98305696],
       [0.9746391 ],
       [0.923527  ],
       [0.08624077]], dtype=float32)

In [87]:

# Convert prediction probabilities to labels
model_6_preds = tf.squeeze(tf.round(model_6_pred_probs))
model_6_preds[:10]

# Convert prediction probabilities to labels model_6_preds = tf.squeeze(tf.round(model_6_pred_probs)) model_6_preds[:10]

Out[87]:

<tf.Tensor: shape=(10,), dtype=float32, numpy=array([0., 1., 1., 0., 1., 1., 1., 1., 1., 0.], dtype=float32)>

In [88]:

# Calculate model 6 performance metrics
model_6_results = calculate_results(val_labels, model_6_preds)
model_6_results

# Calculate model 6 performance metrics model_6_results = calculate_results(val_labels, model_6_preds) model_6_results

Out[88]:

{'accuracy': 81.75853018372703,
 'precision': 0.8206021490415145,
 'recall': 0.8175853018372703,
 'f1': 0.8158792847350168}

In [89]:

# Compare TF Hub model to baseline
compare_baseline_to_new_results(baseline_results, model_6_results)

# Compare TF Hub model to baseline compare_baseline_to_new_results(baseline_results, model_6_results)

Baseline accuracy: 79.27, New accuracy: 81.76, Difference: 2.49
Baseline precision: 0.81, New precision: 0.82, Difference: 0.01
Baseline recall: 0.79, New recall: 0.82, Difference: 0.02
Baseline f1: 0.79, New f1: 0.82, Difference: 0.03

Model 7: TensorFlow Hub Pretrained Sentence Encoder 10% of the training data¶

One of the benefits of using transfer learning methods, such as, the pretrained embeddings within the USE is the ability to get great results on a small amount of data (the USE paper even mentions this in the abstract).

To put this to the test, we're going to make a small subset of the training data (10%), train a model and evaluate it.

In [90]:

### NOTE: Making splits like this will lead to data leakage ###
### (some of the training examples in the validation set) ###

### WRONG WAY TO MAKE SPLITS (train_df_shuffled has already been split) ### 

# # Create subsets of 10% of the training data
# train_10_percent = train_df_shuffled[["text", "target"]].sample(frac=0.1, random_state=42)
# train_sentences_10_percent = train_10_percent["text"].to_list()
# train_labels_10_percent = train_10_percent["target"].to_list()
# len(train_sentences_10_percent), len(train_labels_10_percent)

### NOTE: Making splits like this will lead to data leakage ### ### (some of the training examples in the validation set) ### ### WRONG WAY TO MAKE SPLITS (train_df_shuffled has already been split) ### # # Create subsets of 10% of the training data # train_10_percent = train_df_shuffled[["text", "target"]].sample(frac=0.1, random_state=42) # train_sentences_10_percent = train_10_percent["text"].to_list() # train_labels_10_percent = train_10_percent["target"].to_list() # len(train_sentences_10_percent), len(train_labels_10_percent)

In [91]:

# One kind of correct way (there are more) to make data subset
# (split the already split train_sentences/train_labels)
train_sentences_90_percent, train_sentences_10_percent, train_labels_90_percent, train_labels_10_percent = train_test_split(np.array(train_sentences),
                                                                                                                            train_labels,
                                                                                                                            test_size=0.1,
                                                                                                                            random_state=42)

# One kind of correct way (there are more) to make data subset # (split the already split train_sentences/train_labels) train_sentences_90_percent, train_sentences_10_percent, train_labels_90_percent, train_labels_10_percent = train_test_split(np.array(train_sentences), train_labels, test_size=0.1, random_state=42)

In [92]:

# Check length of 10 percent datasets
print(f"Total training examples: {len(train_sentences)}")
print(f"Length of 10% training examples: {len(train_sentences_10_percent)}")

# Check length of 10 percent datasets print(f"Total training examples: {len(train_sentences)}") print(f"Length of 10% training examples: {len(train_sentences_10_percent)}")

Total training examples: 6851
Length of 10% training examples: 686

Because we've selected a random subset of the training samples, the classes should be roughly balanced (as they are in the full training dataset).

In [93]:

# Check the number of targets in our subset of data 
# (this should be close to the distribution of labels in the original train_labels)
pd.Series(train_labels_10_percent).value_counts()

# Check the number of targets in our subset of data # (this should be close to the distribution of labels in the original train_labels) pd.Series(train_labels_10_percent).value_counts()

Out[93]:

0    415
1    271
dtype: int64

To make sure we're making an appropriate comparison between our model's ability to learn from the full training set and 10% subset, we'll clone our USE model (model_6) using the tf.keras.models.clone_model() method.

Doing this will create the same architecture but reset the learned weights of the clone target (pretrained weights from the USE will remain but all others will be reset).

In [94]:

# Clone model_6 but reset weights
model_7 = tf.keras.models.clone_model(model_6)

# Compile model
model_7.compile(loss="binary_crossentropy",
                optimizer=tf.keras.optimizers.Adam(),
                metrics=["accuracy"])

# Get a summary (will be same as model_6)
model_7.summary()

# Clone model_6 but reset weights model_7 = tf.keras.models.clone_model(model_6) # Compile model model_7.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Adam(), metrics=["accuracy"]) # Get a summary (will be same as model_6) model_7.summary()

Model: "model_6_USE"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 USE (KerasLayer)            (None, 512)               256797824 
                                                                 
 dense_5 (Dense)             (None, 64)                32832     
                                                                 
 dense_6 (Dense)             (None, 1)                 65        
                                                                 
=================================================================
Total params: 256,830,721
Trainable params: 32,897
Non-trainable params: 256,797,824
_________________________________________________________________

Notice the layout of model_7 is the same as model_6. Now let's train the newly created model on our 10% training data subset.

In [95]:

# Fit the model to 10% of the training data
model_7_history = model_7.fit(x=train_sentences_10_percent,
                              y=train_labels_10_percent,
                              epochs=5,
                              validation_data=(val_sentences, val_labels),
                              callbacks=[create_tensorboard_callback(SAVE_DIR, "10_percent_tf_hub_sentence_encoder")])

# Fit the model to 10% of the training data model_7_history = model_7.fit(x=train_sentences_10_percent, y=train_labels_10_percent, epochs=5, validation_data=(val_sentences, val_labels), callbacks=[create_tensorboard_callback(SAVE_DIR, "10_percent_tf_hub_sentence_encoder")])

Saving TensorBoard log files to: model_logs/10_percent_tf_hub_sentence_encoder/20230526-001758
Epoch 1/5
22/22 [==============================] - 4s 41ms/step - loss: 0.6671 - accuracy: 0.6997 - val_loss: 0.6443 - val_accuracy: 0.7415
Epoch 2/5
22/22 [==============================] - 0s 18ms/step - loss: 0.5895 - accuracy: 0.8309 - val_loss: 0.5846 - val_accuracy: 0.7467
Epoch 3/5
22/22 [==============================] - 0s 18ms/step - loss: 0.5116 - accuracy: 0.8382 - val_loss: 0.5336 - val_accuracy: 0.7677
Epoch 4/5
22/22 [==============================] - 0s 18ms/step - loss: 0.4492 - accuracy: 0.8411 - val_loss: 0.5040 - val_accuracy: 0.7703
Epoch 5/5
22/22 [==============================] - 0s 18ms/step - loss: 0.4080 - accuracy: 0.8469 - val_loss: 0.4880 - val_accuracy: 0.7703

Due to the smaller amount of training data, training happens even quicker than before.

Let's evaluate our model's performance after learning on 10% of the training data.

In [96]:

# Make predictions with the model trained on 10% of the data
model_7_pred_probs = model_7.predict(val_sentences)
model_7_pred_probs[:10]

# Make predictions with the model trained on 10% of the data model_7_pred_probs = model_7.predict(val_sentences) model_7_pred_probs[:10]

24/24 [==============================] - 1s 7ms/step

Out[96]:

array([[0.24178001],
       [0.8116845 ],
       [0.91511923],
       [0.32094172],
       [0.587357  ],
       [0.82938445],
       [0.8401675 ],
       [0.8496708 ],
       [0.8371127 ],
       [0.14010696]], dtype=float32)

In [97]:

# Convert prediction probabilities to labels
model_7_preds = tf.squeeze(tf.round(model_7_pred_probs))
model_7_preds[:10]

# Convert prediction probabilities to labels model_7_preds = tf.squeeze(tf.round(model_7_pred_probs)) model_7_preds[:10]

Out[97]:

<tf.Tensor: shape=(10,), dtype=float32, numpy=array([0., 1., 1., 0., 1., 1., 1., 1., 1., 0.], dtype=float32)>

In [98]:

# Calculate model results
model_7_results = calculate_results(val_labels, model_7_preds)
model_7_results

# Calculate model results model_7_results = calculate_results(val_labels, model_7_preds) model_7_results

Out[98]:

{'accuracy': 77.03412073490814,
 'precision': 0.7760118694840564,
 'recall': 0.7703412073490814,
 'f1': 0.7665375100103654}

In [99]:

# Compare to baseline
compare_baseline_to_new_results(baseline_results, model_7_results)

# Compare to baseline compare_baseline_to_new_results(baseline_results, model_7_results)

Baseline accuracy: 79.27, New accuracy: 77.03, Difference: -2.23
Baseline precision: 0.81, New precision: 0.78, Difference: -0.04
Baseline recall: 0.79, New recall: 0.77, Difference: -0.02
Baseline f1: 0.79, New f1: 0.77, Difference: -0.02

Comparing the performance of each of our models¶

Woah. We've come a long way! From training a baseline to several deep models.

Now it's time to compare our model's results.

But just before we do, it's worthwhile mentioning, this type of practice is a standard deep learning workflow. Training various different models, then comparing them to see which one performed best and continuing to train it if necessary.

The important thing to note is that for all of our modelling experiments we used the same training data (except for model_7 where we used 10% of the training data).

To visualize our model's performances, let's create a pandas DataFrame we our results dictionaries and then plot it.

In [100]:

# Combine model results into a DataFrame
all_model_results = pd.DataFrame({"baseline": baseline_results,
                                  "simple_dense": model_1_results,
                                  "lstm": model_2_results,
                                  "gru": model_3_results,
                                  "bidirectional": model_4_results,
                                  "conv1d": model_5_results,
                                  "tf_hub_sentence_encoder": model_6_results,
                                  "tf_hub_10_percent_data": model_7_results})
all_model_results = all_model_results.transpose()
all_model_results

# Combine model results into a DataFrame all_model_results = pd.DataFrame({"baseline": baseline_results, "simple_dense": model_1_results, "lstm": model_2_results, "gru": model_3_results, "bidirectional": model_4_results, "conv1d": model_5_results, "tf_hub_sentence_encoder": model_6_results, "tf_hub_10_percent_data": model_7_results}) all_model_results = all_model_results.transpose() all_model_results

Out[100]:

	accuracy	precision	recall	f1
baseline	79.265092	0.811139	0.792651	0.786219
simple_dense	78.608924	0.790328	0.786089	0.783297
lstm	75.590551	0.756716	0.755906	0.753960
gru	77.559055	0.776327	0.775591	0.774090
bidirectional	76.771654	0.767545	0.767717	0.766793
conv1d	78.740157	0.790061	0.787402	0.785228
tf_hub_sentence_encoder	81.758530	0.820602	0.817585	0.815879
tf_hub_10_percent_data	77.034121	0.776012	0.770341	0.766538

In [101]:

# Reduce the accuracy to same scale as other metrics
all_model_results["accuracy"] = all_model_results["accuracy"]/100

# Reduce the accuracy to same scale as other metrics all_model_results["accuracy"] = all_model_results["accuracy"]/100

In [102]:

# Plot and compare all of the model results
all_model_results.plot(kind="bar", figsize=(10, 7)).legend(bbox_to_anchor=(1.0, 1.0));

# Plot and compare all of the model results all_model_results.plot(kind="bar", figsize=(10, 7)).legend(bbox_to_anchor=(1.0, 1.0));

Looks like our pretrained USE TensorFlow Hub models have the best performance, even the one with only 10% of the training data seems to outperform the other models. This goes to show the power of transfer learning.

How about we drill down and get the F1-score's of each model?

In [103]:

# Sort model results by f1-score
all_model_results.sort_values("f1", ascending=False)["f1"].plot(kind="bar", figsize=(10, 7));

# Sort model results by f1-score all_model_results.sort_values("f1", ascending=False)["f1"].plot(kind="bar", figsize=(10, 7));

Drilling down into a single metric we see our USE TensorFlow Hub models performing better than all of the other models. Interestingly, the baseline's F1-score isn't too far off the rest of the deeper models.

We can also visualize all of our model's training logs using TensorBoard.dev.

In [104]:

# # View tensorboard logs of transfer learning modelling experiments (should be 4 models)
# # Upload TensorBoard dev records
# !tensorboard dev upload --logdir ./model_logs \
#   --name "NLP modelling experiments" \
#   --description "A series of different NLP modellings experiments with various models" \
#   --one_shot # exits the uploader when upload has finished

# # View tensorboard logs of transfer learning modelling experiments (should be 4 models) # # Upload TensorBoard dev records # !tensorboard dev upload --logdir ./model_logs \ # --name "NLP modelling experiments" \ # --description "A series of different NLP modellings experiments with various models" \ # --one_shot # exits the uploader when upload has finished

The TensorBoard logs of the different modelling experiments we ran can be viewed here: https://tensorboard.dev/experiment/LkoAakb7QIKBZ0RL97cXbw/

In [105]:

# If you need to remove previous experiments, you can do so using the following command
# !tensorboard dev delete --experiment_id EXPERIMENT_ID_TO_DELETE

# If you need to remove previous experiments, you can do so using the following command # !tensorboard dev delete --experiment_id EXPERIMENT_ID_TO_DELETE

Combining our models (model ensembling/stacking)¶

Many production systems use an ensemble (multiple different models combined) of models to make a prediction.

The idea behind model stacking is that if several uncorrelated models agree on a prediction, then the prediction must be more robust than a prediction made by a singular model.

The keyword in the sentence above is uncorrelated, which is another way of saying, different types of models. For example, in our case, we might combine our baseline, our bidirectional model and our TensorFlow Hub USE model.

Although these models are all trained on the same data, they all have a different way of finding patterns.

If we were to use three similarly trained models, such as three LSTM models, the predictions they output will likely be very similar.

Think of it as trying to decide where to eat with your friends. If you all have similar tastes, you'll probably all pick the same restaurant. But if you've all got different tastes and still end up picking the same restaurant, the restaurant must be good.

Since we're working with a classification problem, there are a few of ways we can combine our models:

1. Averaging - Take the output prediction probabilities of each model for each sample, combine them and then average them.
2. Majority vote (mode) - Make class predictions with each of your models on all samples, the predicted class is the one in majority. For example, if three different models predict [1, 0, 1] respectively, the majority class is 1, therefore, that would be the predicted label.
3. Model stacking - Take the outputs of each of your chosen models and use them as inputs to another model.

📖 Resource: The above methods for model stacking/ensembling were adapted from Chapter 6 of the Machine Learning Engineering Book by Andriy Burkov. If you're looking to enter the field of machine learning engineering, not only building models but production-scale machine learning systems, I'd highly recommend reading it in its entirety.

Again, the concept of model stacking is best seen in action.

We're going to combine our baseline model (model_0), LSTM model (model_2) and our USE model trained on the full training data (model_6) by averaging the combined prediction probabilities of each.

In [106]:

# Get mean pred probs for 3 models
baseline_pred_probs = np.max(model_0.predict_proba(val_sentences), axis=1) # get the prediction probabilities from baseline model
combined_pred_probs = baseline_pred_probs + tf.squeeze(model_2_pred_probs, axis=1) + tf.squeeze(model_6_pred_probs)
combined_preds = tf.round(combined_pred_probs/3) # average and round the prediction probabilities to get prediction classes
combined_preds[:20]

# Get mean pred probs for 3 models baseline_pred_probs = np.max(model_0.predict_proba(val_sentences), axis=1) # get the prediction probabilities from baseline model combined_pred_probs = baseline_pred_probs + tf.squeeze(model_2_pred_probs, axis=1) + tf.squeeze(model_6_pred_probs) combined_preds = tf.round(combined_pred_probs/3) # average and round the prediction probabilities to get prediction classes combined_preds[:20]

Out[106]:

<tf.Tensor: shape=(20,), dtype=float32, numpy=
array([0., 1., 1., 0., 0., 1., 1., 1., 1., 0., 0., 1., 0., 1., 0., 0., 0.,
       0., 0., 1.], dtype=float32)>

Wonderful! We've got a combined predictions array of different classes, let's evaluate them against the true labels and add our stacked model's results to our all_model_results DataFrame.

In [107]:

# Calculate results from averaging the prediction probabilities
ensemble_results = calculate_results(val_labels, combined_preds)
ensemble_results

# Calculate results from averaging the prediction probabilities ensemble_results = calculate_results(val_labels, combined_preds) ensemble_results

Out[107]:

{'accuracy': 77.95275590551181,
 'precision': 0.7792442137914578,
 'recall': 0.7795275590551181,
 'f1': 0.7789463852322546}

In [108]:

# Add our combined model's results to the results DataFrame
all_model_results.loc["ensemble_results"] = ensemble_results

# Add our combined model's results to the results DataFrame all_model_results.loc["ensemble_results"] = ensemble_results

In [109]:

# Convert the accuracy to the same scale as the rest of the results
all_model_results.loc["ensemble_results"]["accuracy"] = all_model_results.loc["ensemble_results"]["accuracy"]/100

# Convert the accuracy to the same scale as the rest of the results all_model_results.loc["ensemble_results"]["accuracy"] = all_model_results.loc["ensemble_results"]["accuracy"]/100

In [110]:

all_model_results

all_model_results

Out[110]:

	accuracy	precision	recall	f1
baseline	0.792651	0.811139	0.792651	0.786219
simple_dense	0.786089	0.790328	0.786089	0.783297
lstm	0.755906	0.756716	0.755906	0.753960
gru	0.775591	0.776327	0.775591	0.774090
bidirectional	0.767717	0.767545	0.767717	0.766793
conv1d	0.787402	0.790061	0.787402	0.785228
tf_hub_sentence_encoder	0.817585	0.820602	0.817585	0.815879
tf_hub_10_percent_data	0.770341	0.776012	0.770341	0.766538
ensemble_results	0.779528	0.779244	0.779528	0.778946

How did the stacked model go against the other models?

🔑 Note: It seems many of our model's results are similar. This may mean there are some limitations to what can be learned from our data. When many of your modelling experiments return similar results, it's a good idea to revisit your data, we'll do this shortly.

Saving and loading a trained model¶

Although training time didn't take very long, it's good practice to save your trained models to avoid having to retrain them.

Saving your models also enables you to export them for use elsewhere outside of your notebooks, such as in a web application.

There are two main ways of saving a model in TensorFlow:

1. The HDF5 format.
2. The SavedModel format (default).

Let's take a look at both.

In [111]:

# Save TF Hub Sentence Encoder model to HDF5 format
model_6.save("model_6.h5")

# Save TF Hub Sentence Encoder model to HDF5 format model_6.save("model_6.h5")

If you save a model as a HDF5, when loading it back in, you need to let TensorFlow know about any custom objects you've used (e.g. components which aren't built from pure TensorFlow, such as TensorFlow Hub components).

In [112]:

# Load model with custom Hub Layer (required with HDF5 format)
loaded_model_6 = tf.keras.models.load_model("model_6.h5", 
                                            custom_objects={"KerasLayer": hub.KerasLayer})

# Load model with custom Hub Layer (required with HDF5 format) loaded_model_6 = tf.keras.models.load_model("model_6.h5", custom_objects={"KerasLayer": hub.KerasLayer})

In [113]:

# How does our loaded model perform?
loaded_model_6.evaluate(val_sentences, val_labels)

# How does our loaded model perform? loaded_model_6.evaluate(val_sentences, val_labels)

24/24 [==============================] - 1s 7ms/step - loss: 0.4299 - accuracy: 0.8176

Out[113]:

[0.4298648238182068, 0.817585289478302]

Calling the save() method on our target model and passing it a filepath allows us to save our model in the SavedModel format.

In [114]:

# Save TF Hub Sentence Encoder model to SavedModel format (default)
model_6.save("model_6_SavedModel_format")

# Save TF Hub Sentence Encoder model to SavedModel format (default) model_6.save("model_6_SavedModel_format")

WARNING:absl:Function `_wrapped_model` contains input name(s) USE_input with unsupported characters which will be renamed to use_input in the SavedModel.

If you use SavedModel format (default), you can reload your model without specifying custom objects using the tensorflow.keras.models.load_model() function.

In [115]:

# Load TF Hub Sentence Encoder SavedModel
loaded_model_6_SavedModel = tf.keras.models.load_model("model_6_SavedModel_format")

# Load TF Hub Sentence Encoder SavedModel loaded_model_6_SavedModel = tf.keras.models.load_model("model_6_SavedModel_format")

In [116]:

# Evaluate loaded SavedModel format
loaded_model_6_SavedModel.evaluate(val_sentences, val_labels)

# Evaluate loaded SavedModel format loaded_model_6_SavedModel.evaluate(val_sentences, val_labels)

24/24 [==============================] - 1s 8ms/step - loss: 0.4299 - accuracy: 0.8176

Out[116]:

[0.4298648238182068, 0.817585289478302]

As you can see saving and loading our model with either format results in the same performance.

🤔 Question: Should you used the SavedModel format or HDF5 format?

For most use cases, the SavedModel format will suffice. However, this is a TensorFlow specific standard. If you need a more general-purpose data standard, HDF5 might be better. For more, check out the TensorFlow documentation on saving and loading models.

Finding the most wrong examples¶

We mentioned before that if many of our modelling experiments are returning similar results, despite using different kinds of models, it's a good idea to return to the data and inspect why this might be.

One of the best ways to inspect your data is to sort your model's predictions and find the samples it got most wrong, meaning, what predictions had a high prediction probability but turned out to be wrong.

Once again, visualization is your friend. Visualize, visualize, visualize.

To make things visual, let's take our best performing model's prediction probabilities and classes along with the validation samples (text and ground truth labels) and combine them in a pandas DataFrame.

• If our best model still isn't perfect, what examples is it getting wrong?
• Which ones are the most wrong?
• Are there some labels which are wrong? E.g. the model gets it right but the ground truth label doesn't reflect this

In [117]:

# Create dataframe with validation sentences and best performing model predictions
val_df = pd.DataFrame({"text": val_sentences,
                       "target": val_labels,
                       "pred": model_6_preds,
                       "pred_prob": tf.squeeze(model_6_pred_probs)})
val_df.head()

# Create dataframe with validation sentences and best performing model predictions val_df = pd.DataFrame({"text": val_sentences, "target": val_labels, "pred": model_6_preds, "pred_prob": tf.squeeze(model_6_pred_probs)}) val_df.head()

Out[117]:

	text	target	pred	pred_prob
0	DFR EP016 Monthly Meltdown - On Dnbheaven 2015...	0	0.0	0.148141
1	FedEx no longer to transport bioterror germs i...	0	1.0	0.740579
2	Gunmen kill four in El Salvador bus attack: Su...	1	1.0	0.988647
3	@camilacabello97 Internally and externally scr...	1	0.0	0.224560
4	Radiation emergency #preparedness starts with ...	1	1.0	0.740494

Oh yeah! Now let's find our model's wrong predictions (where target != pred) and sort them by their prediction probability (the pred_prob column).

In [118]:

# Find the wrong predictions and sort by prediction probabilities
most_wrong = val_df[val_df["target"] != val_df["pred"]].sort_values("pred_prob", ascending=False)
most_wrong[:10]

# Find the wrong predictions and sort by prediction probabilities most_wrong = val_df[val_df["target"] != val_df["pred"]].sort_values("pred_prob", ascending=False) most_wrong[:10]

Out[118]:

	text	target	pred	pred_prob
31	? High Skies - Burning Buildings ? http://t.co...	0	1.0	0.906832
628	@noah_anyname That's where the concentration c...	0	1.0	0.866348
759	FedEx will no longer transport bioterror patho...	0	1.0	0.859502
393	@SonofLiberty357 all illuminated by the bright...	0	1.0	0.855963
49	@madonnamking RSPCA site multiple 7 story high...	0	1.0	0.839930
209	Ashes 2015: Australia‰Ûªs collapse at Trent Br...	0	1.0	0.815515
251	@AshGhebranious civil rights continued in the ...	0	1.0	0.807973
109	[55436] 1950 LIONEL TRAINS SMOKE LOCOMOTIVES W...	0	1.0	0.806746
698	åÈMGN-AFRICAå¨ pin:263789F4 åÈ Correction: Ten...	0	1.0	0.782425
695	A look at state actions a year after Ferguson'...	0	1.0	0.759534

Finally, we can write some code to visualize the sample text, truth label, prediction class and prediction probability. Because we've sorted our samples by prediction probability, viewing samples from the head of our most_wrong DataFrame will show us false positives.

A reminder:

• 0 = Not a real diaster Tweet
• 1 = Real diaster Tweet

In [119]:

# Check the false positives (model predicted 1 when should've been 0)
for row in most_wrong[:10].itertuples(): # loop through the top 10 rows (change the index to view different rows)
  _, text, target, pred, prob = row
  print(f"Target: {target}, Pred: {int(pred)}, Prob: {prob}")
  print(f"Text:\n{text}\n")
  print("----\n")

# Check the false positives (model predicted 1 when should've been 0) for row in most_wrong[:10].itertuples(): # loop through the top 10 rows (change the index to view different rows) _, text, target, pred, prob = row print(f"Target: {target}, Pred: {int(pred)}, Prob: {prob}") print(f"Text:\n{text}\n") print("----\n")

Target: 0, Pred: 1, Prob: 0.9068315625190735
Text:
? High Skies - Burning Buildings ? http://t.co/uVq41i3Kx2 #nowplaying

----

Target: 0, Pred: 1, Prob: 0.8663479685783386
Text:
@noah_anyname That's where the concentration camps and mass murder come in. 
 
EVERY. FUCKING. TIME.

----

Target: 0, Pred: 1, Prob: 0.859502375125885
Text:
FedEx will no longer transport bioterror pathogens in wake of anthrax lab mishaps http://t.co/lHpgxc4b8J

----

Target: 0, Pred: 1, Prob: 0.8559632897377014
Text:
@SonofLiberty357 all illuminated by the brightly burning buildings all around the town!

----

Target: 0, Pred: 1, Prob: 0.8399295806884766
Text:
@madonnamking RSPCA site multiple 7 story high rise buildings next to low density character residential in an area that floods

----

Target: 0, Pred: 1, Prob: 0.8155148029327393
Text:
Ashes 2015: Australia‰Ûªs collapse at Trent Bridge among worst in history: England bundled out Australia for 60 ... http://t.co/t5TrhjUAU0

----

Target: 0, Pred: 1, Prob: 0.8079732060432434
Text:
@AshGhebranious civil rights continued in the 60s. And what about trans-generational trauma? if anything we should listen to the Americans.

----

Target: 0, Pred: 1, Prob: 0.8067457675933838
Text:
[55436] 1950 LIONEL TRAINS SMOKE LOCOMOTIVES WITH MAGNE-TRACTION INSTRUCTIONS http://t.co/xEZBs3sq0y http://t.co/C2x0QoKGlY

----

Target: 0, Pred: 1, Prob: 0.7824245095252991
Text:
åÈMGN-AFRICAå¨ pin:263789F4 åÈ Correction: Tent Collapse Story: Correction: Tent Collapse story åÈ http://t.co/fDJUYvZMrv @wizkidayo

----

Target: 0, Pred: 1, Prob: 0.7595335841178894
Text:
A look at state actions a year after Ferguson's upheaval http://t.co/GZEkQWzijq

----

We can view the bottom end of our most_wrong DataFrame to inspect false negatives (model predicts 0, not a real diaster Tweet, when it should've predicted 1, real diaster Tweet).

In [120]:

# Check the most wrong false negatives (model predicted 0 when should've predict 1)
for row in most_wrong[-10:].itertuples():
  _, text, target, pred, prob = row
  print(f"Target: {target}, Pred: {int(pred)}, Prob: {prob}")
  print(f"Text:\n{text}\n")
  print("----\n")

# Check the most wrong false negatives (model predicted 0 when should've predict 1) for row in most_wrong[-10:].itertuples(): _, text, target, pred, prob = row print(f"Target: {target}, Pred: {int(pred)}, Prob: {prob}") print(f"Text:\n{text}\n") print("----\n")

Target: 1, Pred: 0, Prob: 0.06247330829501152
Text:
going to redo my nails and watch behind the scenes of desolation of smaug ayyy

----

Target: 1, Pred: 0, Prob: 0.05949299782514572
Text:
@BoyInAHorsemask its a panda trapped in a dogs body

----

Target: 1, Pred: 0, Prob: 0.056083984673023224
Text:
@willienelson We need help! Horses will die!Please RT & sign petition!Take a stand & be a voice for them! #gilbert23 https://t.co/e8dl1lNCVu

----

Target: 1, Pred: 0, Prob: 0.055036477744579315
Text:
Lucas Duda is Ghost Rider. Not the Nic Cage version but an actual 'engulfed in flames' badass. #Mets

----

Target: 1, Pred: 0, Prob: 0.054454777389764786
Text:
You can never escape me. Bullets don't harm me. Nothing harms me. But I know pain. I know pain. Sometimes I share it. With someone like you.

----

Target: 1, Pred: 0, Prob: 0.046157706528902054
Text:
I get to smoke my shit in peace

----

Target: 1, Pred: 0, Prob: 0.03960023820400238
Text:
Why are you deluged with low self-image? Take the quiz: http://t.co/XsPqdOrIqj http://t.co/CQYvFR4UCy

----

Target: 1, Pred: 0, Prob: 0.03830057382583618
Text:
Ron & Fez - Dave's High School Crush https://t.co/aN3W16c8F6 via @YouTube

----

Target: 1, Pred: 0, Prob: 0.03802212327718735
Text:
@SoonerMagic_ I mean I'm a fan but I don't need a girl sounding off like a damn siren

----

Target: 1, Pred: 0, Prob: 0.03466600552201271
Text:
Reddit Will Now Quarantine‰Û_ http://t.co/pkUAMXw6pm #onlinecommunities #reddit #amageddon #freespeech #Business http://t.co/PAWvNJ4sAP

----

Do you notice anything interesting about the most wrong samples?

Are the ground truth labels correct? What do you think would happen if we went back and corrected the labels which aren't?

Making predictions on the test dataset¶

Alright we've seen how our model's perform on the validation set.

But how about the test dataset?

We don't have labels for the test dataset so we're going to have to make some predictions and inspect them for ourselves.

Let's write some code to make predictions on random samples from the test dataset and visualize them.

In [121]:

# Making predictions on the test dataset
test_sentences = test_df["text"].to_list()
test_samples = random.sample(test_sentences, 10)
for test_sample in test_samples:
  pred_prob = tf.squeeze(model_6.predict([test_sample])) # has to be list
  pred = tf.round(pred_prob)
  print(f"Pred: {int(pred)}, Prob: {pred_prob}")
  print(f"Text:\n{test_sample}\n")
  print("----\n")

# Making predictions on the test dataset test_sentences = test_df["text"].to_list() test_samples = random.sample(test_sentences, 10) for test_sample in test_samples: pred_prob = tf.squeeze(model_6.predict([test_sample])) # has to be list pred = tf.round(pred_prob) print(f"Pred: {int(pred)}, Prob: {pred_prob}") print(f"Text:\n{test_sample}\n") print("----\n")

1/1 [==============================] - 0s 79ms/step
Pred: 0, Prob: 0.05416637659072876
Text:
WHAT a day's cricket that was. Has destroyed any plans I had for exercise today.

----

1/1 [==============================] - 0s 39ms/step
Pred: 1, Prob: 0.5330829620361328
Text:
Any other generation this would've been fatality  http://t.co/zcCtZM9f0o

----

1/1 [==============================] - 0s 40ms/step
Pred: 1, Prob: 0.9940084218978882
Text:
Arson suspect linked to 30 fires caught in Northern California http://t.co/HkFPyNb4PS

----

1/1 [==============================] - 0s 40ms/step
Pred: 1, Prob: 0.9726524353027344
Text:
Help support the victims of the Japanese Earthquake and Pacific Tsunami http://t.co/O5GbPBQH http://t.co/MN5wnxf0 #hope4japan #pray4japan

----

1/1 [==============================] - 0s 40ms/step
Pred: 0, Prob: 0.36651405692100525
Text:
this is from my show last night and im still panicking over the fact i saw sweaty ashton with my own two eyes http://t.co/yyJ76WBC9y

----

1/1 [==============================] - 0s 41ms/step
Pred: 0, Prob: 0.42949625849723816
Text:
He came to a land which was engulfed in tribal war and turned it into a land of peace i.e. Madinah. #ProphetMuhammad #islam

----

1/1 [==============================] - 0s 41ms/step
Pred: 1, Prob: 0.7450974583625793
Text:
Jane Kelsey on the FIRE Economy
5th Aug 5:30‰ÛÒ7:30pm
Old Govt Buildings Wgton
The context & the driver for #TPP and #TRADEinSERVICESAgreement

----

1/1 [==============================] - 0s 41ms/step
Pred: 0, Prob: 0.13024944067001343
Text:
Detonation fashionable mountaineering electronic watch water-resistant couples leisure tab‰Û_ http://t.co/GH48B54riS http://t.co/2PqTm06Lid

----

1/1 [==============================] - 0s 41ms/step
Pred: 1, Prob: 0.8552481532096863
Text:
@AlbertBrooks Don't like the Ayatollah Khomeini Memorial Nuclear Reactor for the Annihilation of Israel? Racist!

----

1/1 [==============================] - 0s 40ms/step
Pred: 0, Prob: 0.06269928067922592
Text:
Can you imagine how traumatised Makoto would be if he could see himself in the dub (aka Jersey Shore AU) rn? Well done America

----

How do our model's predictions look on the test dataset?

It's important to do these kind of visualization checks as often as possible to get a glance of how your model performs on unseen data and subsequently how it might perform on the real test: Tweets from the wild.

Predicting on Tweets from the wild¶

How about we find some Tweets and use our model to predict whether or not they're about a diaster or not?

To start, let's take one of my own Tweets on living life like an ensemble model.

In [122]:

# Turn Tweet into string
daniels_tweet = "Life like an ensemble: take the best choices from others and make your own"

# Turn Tweet into string daniels_tweet = "Life like an ensemble: take the best choices from others and make your own"

Now we'll write a small function to take a model and an example sentence and return a prediction.

In [123]:

def predict_on_sentence(model, sentence):
  """
  Uses model to make a prediction on sentence.

  Returns the sentence, the predicted label and the prediction probability.
  """
  pred_prob = model.predict([sentence])
  pred_label = tf.squeeze(tf.round(pred_prob)).numpy()
  print(f"Pred: {pred_label}", "(real disaster)" if pred_label > 0 else "(not real disaster)", f"Prob: {pred_prob[0][0]}")
  print(f"Text:\n{sentence}")

def predict_on_sentence(model, sentence): """ Uses model to make a prediction on sentence. Returns the sentence, the predicted label and the prediction probability. """ pred_prob = model.predict([sentence]) pred_label = tf.squeeze(tf.round(pred_prob)).numpy() print(f"Pred: {pred_label}", "(real disaster)" if pred_label > 0 else "(not real disaster)", f"Prob: {pred_prob[0][0]}") print(f"Text:\n{sentence}")

Great! Time to test our model out.

In [124]:

# Make a prediction on Tweet from the wild
predict_on_sentence(model=model_6, # use the USE model
                    sentence=daniels_tweet)

# Make a prediction on Tweet from the wild predict_on_sentence(model=model_6, # use the USE model sentence=daniels_tweet)

1/1 [==============================] - 0s 39ms/step
Pred: 0.0 (not real disaster) Prob: 0.044768452644348145
Text:
Life like an ensemble: take the best choices from others and make your own

Woohoo! Our model predicted correctly. My Tweet wasn't about a diaster.

How about we find a few Tweets about actual diasters?

Such as the following two Tweets about the 2020 Beirut explosions.

In [125]:

# Source - https://twitter.com/BeirutCityGuide/status/1290696551376007168
beirut_tweet_1 = "Reports that the smoke in Beirut sky contains nitric acid, which is toxic. Please share and refrain from stepping outside unless urgent. #Lebanon"

# Source - https://twitter.com/BeirutCityGuide/status/1290773498743476224
beirut_tweet_2 = "#Beirut declared a “devastated city”, two-week state of emergency officially declared. #Lebanon"

# Source - https://twitter.com/BeirutCityGuide/status/1290696551376007168 beirut_tweet_1 = "Reports that the smoke in Beirut sky contains nitric acid, which is toxic. Please share and refrain from stepping outside unless urgent. #Lebanon" # Source - https://twitter.com/BeirutCityGuide/status/1290773498743476224 beirut_tweet_2 = "#Beirut declared a “devastated city”, two-week state of emergency officially declared. #Lebanon"

In [126]:

# Predict on diaster Tweet 1
predict_on_sentence(model=model_6, 
                    sentence=beirut_tweet_1)

# Predict on diaster Tweet 1 predict_on_sentence(model=model_6, sentence=beirut_tweet_1)

1/1 [==============================] - 0s 42ms/step
Pred: 1.0 (real disaster) Prob: 0.9650391936302185
Text:
Reports that the smoke in Beirut sky contains nitric acid, which is toxic. Please share and refrain from stepping outside unless urgent. #Lebanon

In [127]:

# Predict on diaster Tweet 2
predict_on_sentence(model=model_6, 
                    sentence=beirut_tweet_2)

# Predict on diaster Tweet 2 predict_on_sentence(model=model_6, sentence=beirut_tweet_2)

1/1 [==============================] - 0s 40ms/step
Pred: 1.0 (real disaster) Prob: 0.9686568379402161
Text:
#Beirut declared a “devastated city”, two-week state of emergency officially declared. #Lebanon

Looks like our model is performing as expected, predicting both of the diaster Tweets as actual diasters.

🔑 Note: The above examples are cherry-picked and are cases where you'd expect a model to function at high performance. For actual production systems, you'll want to continaully perform tests to see how your model is performing.

The speed/score tradeoff¶

One of the final tests we're going to do is to find the speed/score tradeoffs between our best model and baseline model.

Why is this important?

Although it can be tempting to just choose the best performing model you find through experimentation, this model might not actually work in a production setting.

Put it this way, imagine you're Twitter and receive 1 million Tweets per hour (this is a made up number, the actual number is much higher). And you're trying to build a diaster detection system to read Tweets and alert authorities with details about a diaster in close to real-time.

Compute power isn't free so you're limited to a single compute machine for the project. On that machine, one of your models makes 10,000 predictions per second at 80% accuracy where as another one of your models (a larger model) makes 100 predictions per second at 85% accuracy.

Which model do you choose?

Is the second model's performance boost worth missing out on the extra capacity?

Of course, there are many options you could try here, such as sending as many Tweets as possible to the first model and then sending the ones which the model is least certain of to the second model.

The point here is to illustrate the best model you find through experimentation, might not be the model you end up using in production.

To make this more concrete, let's write a function to take a model and a number of samples and time how long the given model takes to make predictions on those samples.

In [128]:

# Calculate the time of predictions
import time
def pred_timer(model, samples):
  """
  Times how long a model takes to make predictions on samples.
  
  Args:
  ----
  model = a trained model
  sample = a list of samples

  Returns:
  ----
  total_time = total elapsed time for model to make predictions on samples
  time_per_pred = time in seconds per single sample
  """
  start_time = time.perf_counter() # get start time
  model.predict(samples) # make predictions
  end_time = time.perf_counter() # get finish time
  total_time = end_time-start_time # calculate how long predictions took to make
  time_per_pred = total_time/len(val_sentences) # find prediction time per sample
  return total_time, time_per_pred

# Calculate the time of predictions import time def pred_timer(model, samples): """ Times how long a model takes to make predictions on samples. Args: ---- model = a trained model sample = a list of samples Returns: ---- total_time = total elapsed time for model to make predictions on samples time_per_pred = time in seconds per single sample """ start_time = time.perf_counter() # get start time model.predict(samples) # make predictions end_time = time.perf_counter() # get finish time total_time = end_time-start_time # calculate how long predictions took to make time_per_pred = total_time/len(val_sentences) # find prediction time per sample return total_time, time_per_pred

Looking good!

Now let's use our pred_timer() function to evaluate the prediction times of our best performing model (model_6) and our baseline model (model_0).

In [129]:

# Calculate TF Hub Sentence Encoder prediction times
model_6_total_pred_time, model_6_time_per_pred = pred_timer(model_6, val_sentences)
model_6_total_pred_time, model_6_time_per_pred

# Calculate TF Hub Sentence Encoder prediction times model_6_total_pred_time, model_6_time_per_pred = pred_timer(model_6, val_sentences) model_6_total_pred_time, model_6_time_per_pred

24/24 [==============================] - 0s 7ms/step

Out[129]:

(0.2243557769999711, 0.0002944301535432692)

In [130]:

# Calculate Naive Bayes prediction times
baseline_total_pred_time, baseline_time_per_pred = pred_timer(model_0, val_sentences)
baseline_total_pred_time, baseline_time_per_pred

# Calculate Naive Bayes prediction times baseline_total_pred_time, baseline_time_per_pred = pred_timer(model_0, val_sentences) baseline_total_pred_time, baseline_time_per_pred

Out[130]:

(0.013254724999967493, 1.739465223092847e-05)

It seems with our current hardware (in my case, I'm using a Google Colab notebook) our best performing model takes over 10x the time to make predictions as our baseline model.

Is that extra prediction time worth it?

Let's compare time per prediction versus our model's F1-scores.

In [131]:

import matplotlib.pyplot as plt

plt.figure(figsize=(10, 7))
plt.scatter(baseline_time_per_pred, baseline_results["f1"], label="baseline")
plt.scatter(model_6_time_per_pred, model_6_results["f1"], label="tf_hub_sentence_encoder")
plt.legend()
plt.title("F1-score versus time per prediction")
plt.xlabel("Time per prediction")
plt.ylabel("F1-Score");

import matplotlib.pyplot as plt plt.figure(figsize=(10, 7)) plt.scatter(baseline_time_per_pred, baseline_results["f1"], label="baseline") plt.scatter(model_6_time_per_pred, model_6_results["f1"], label="tf_hub_sentence_encoder") plt.legend() plt.title("F1-score versus time per prediction") plt.xlabel("Time per prediction") plt.ylabel("F1-Score");

Ideal position for speed and performance tradeoff model (fast predictions with great results).

Of course, the ideal position for each of these dots is to be in the top left of the plot (low time per prediction, high F1-score).

In our case, there's a clear tradeoff for time per prediction and performance. Our best performing model takes an order of magnitude longer per prediction but only results in a few F1-score point increase.

This kind of tradeoff is something you'll need to keep in mind when incorporating machine learning models into your own applications.

🛠 Exercises¶

1. Rebuild, compile and train model_1, model_2 and model_5 using the Keras Sequential API instead of the Functional API.
2. Retrain the baseline model with 10% of the training data. How does perform compared to the Universal Sentence Encoder model with 10% of the training data?
3. Try fine-tuning the TF Hub Universal Sentence Encoder model by setting training=True when instantiating it as a Keras layer.

We can use this encoding layer in place of our text_vectorizer and embedding layer

sentence_encoder_layer = hub.KerasLayer("https://tfhub.dev/google/universal-sentence-encoder/4",
                                        input_shape=[],
                                        dtype=tf.string,
                                        trainable=True) # turn training on to fine-tune the TensorFlow Hub model

4. Retrain the best model you've got so far on the whole training set (no validation split). Then use this trained model to make predictions on the test dataset and format the predictions into the same format as the sample_submission.csv file from Kaggle (see the Files tab in Colab for what the sample_submission.csv file looks like). Once you've done this, make a submission to the Kaggle competition, how did your model perform?
5. Combine the ensemble predictions using the majority vote (mode), how does this perform compare to averaging the prediction probabilities of each model?
6. Make a confusion matrix with the best performing model's predictions on the validation set and the validation ground truth labels.

📖 Extra-curriculum¶

To practice what you've learned, a good idea would be to spend an hour on 3 of the following (3-hours total, you could through them all if you want) and then write a blog post about what you've learned.

• For an overview of the different problems within NLP and how to solve them read through:
• A Simple Introduction to Natural Language Processing
• How to solve 90% of NLP problems: a step-by-step guide
• Go through MIT's Recurrent Neural Networks lecture. This will be one of the greatest additions to what's happening behind the RNN model's you've been building.
• Read through the word embeddings page on the TensorFlow website. Embeddings are such a large part of NLP. We've covered them throughout this notebook but extra practice would be well worth it. A good exercise would be to write out all the code in the guide in a new notebook.
• For more on RNN's in TensorFlow, read and reproduce the TensorFlow RNN guide. We've covered many of the concepts in this guide, but it's worth writing the code again for yourself.
• Text data doesn't always come in a nice package like the data we've downloaded. So if you're after more on preparing different text sources for being with your TensorFlow deep learning models, it's worth checking out the following:
• TensorFlow text loading tutorial.
• Reading text files with Python by Real Python.
• This notebook has focused on writing NLP code. For a mathematically rich overview of how NLP with Deep Learning happens, read Standford's Natural Language Processing with Deep Learning lecture notes Part 1.
  • For an even deeper dive, you could even do the whole CS224n (Natural Language Processing with Deep Learning) course.
• Great blog posts to read:
  • Andrei Karpathy's The Unreasonable Effectiveness of RNNs dives into generating Shakespeare text with RNNs.
  • Text Classification with NLP: Tf-Idf vs Word2Vec vs BERT by Mauro Di Pietro. An overview of different techniques for turning text into numbers and then classifying it.
  • What are word embeddings? by Machine Learning Mastery.
• Other topics worth looking into:
  • Attention mechanisms. These are a foundational component of the transformer architecture and also often add improvments to deep NLP models.
  • Transformer architectures. This model architecture has recently taken the NLP world by storm, achieving state of the art on many benchmarks. However, it does take a little more processing to get off the ground, the HuggingFace Models (formerly HuggingFace Transformers) library is probably your best quick start.
    • And now HuggingFace even have their own course on how their library works! I haven't done it but anything HuggingFace makes is world-class.

📖 Resource: See the full set of course materials on GitHub: https://github.com/mrdbourke/tensorflow-deep-learning